题目内容
从正方体ABCD-A1B1C1D1的所有顶点中任取两点连成直线，要求所得直线与AC1垂直，则这样的直线共有________条．
6
分析：连接AC，则BD⊥AC．在正方体ABCD-A1B1C1D1中，由C1C⊥平面BCD，BD?平面BCD，知C1C⊥BD，由此能证明AC1⊥BD．同样地可以证明这样的直线共有 6条．
解答：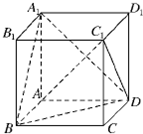
证明：如图，连接AC，则BD⊥AC．
在正方体ABCD-A1B1C1D1中，
∵C1C⊥平面BCD，
BD?平面BCD，
∴C1C⊥BD，
又AC∩CC1=C，
∴BD⊥平面ACC1，
∵AC1?平面ACC1，
∴AC1⊥BD．
同样A1B，A1D，B1D1，B1D，C1D都与AC1垂直．
故答案为：6
点评：本题考查棱柱的结构特征，是中档题．解题时要认真审题，注意挖掘题设中的隐含条件，合理地化空间问题为平面问题．
分析：连接AC，则BD⊥AC．在正方体ABCD-A1B1C1D1中，由C1C⊥平面BCD，BD?平面BCD，知C1C⊥BD，由此能证明AC1⊥BD．同样地可以证明这样的直线共有 6条．
解答：
证明：如图，连接AC，则BD⊥AC．在正方体ABCD-A1B1C1D1中，
∵C1C⊥平面BCD，
BD?平面BCD，
∴C1C⊥BD，
又AC∩CC1=C，
∴BD⊥平面ACC1，
∵AC1?平面ACC1，
∴AC1⊥BD．
同样A1B，A1D，B1D1，B1D，C1D都与AC1垂直．
故答案为：6
点评：本题考查棱柱的结构特征，是中档题．解题时要认真审题，注意挖掘题设中的隐含条件，合理地化空间问题为平面问题．
练习册系列答案
快乐5加2金卷系列答案
相关题目
-4 B.
-8 D.
-12
-12 B.C
-8 C.C
-6 D.C
-4
