题目内容
设i是虚数单位,在复平面上,满足|z+1+i|=2
的复数z对应的点Z的集合是( )
| 2 |
| A、圆 | B、椭圆 | C、双曲线 | D、线段 |
分析:在复平面上,满足|z+1+i|=2
的复数z对应的点Z的集合是:到定点C(-1,-1)的距离等于定值2
的点的集合,即表示的是以点C为圆心,2
为半径的圆.
| 2 |
| 2 |
| 2 |
解答:解:由于|z+1+i|=2
可化为:|z-(-1-i)|=2
,
∴在复平面上,满足|z+1+i|=2
的复数z对应的点Z的集合是:到定点C(-1,-1)的距离等于定值2
的点的集合,即表示的是以点C为圆心,2
为半径的圆.
故选:A.
| 2 |
| 2 |
∴在复平面上,满足|z+1+i|=2
| 2 |
| 2 |
| 2 |
故选:A.
点评:本题考查了复平面上圆的方程的表示形式、复数的几何意义、两点间的距离公式,属于基础题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
设i是虚数单位,在复平面上,满足|z+1+i|+|z-1-i|=2
的复数z对应的点Z的集合是( )
| 2 |
| A、圆 | B、椭圆 | C、双曲线 | D、线段 |
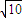 ,且(1+2i)z(i是虚数单位)在复平面上对应的点在直线y=x上,求z.
,且(1+2i)z(i是虚数单位)在复平面上对应的点在直线y=x上,求z.