题目内容
(选做题)
设集合A={x|x2﹣5x+4>0},B={x|x2﹣2ax+(a+2)=0},若A∩B≠ ,求实数a的取值范围.
,求实数a的取值范围.
设集合A={x|x2﹣5x+4>0},B={x|x2﹣2ax+(a+2)=0},若A∩B≠
 ,求实数a的取值范围.
,求实数a的取值范围. 解:A={x|x2﹣5x+4>0}={x|x<1或x>4}.
∵A∩B≠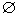 ,
,
∴方程x2﹣2ax+(a+2)=0有解,且至少有一解在区间(﹣∞,1)∪(4,+∞)内
直接求解情况比较多,考虑补集
设全集U={a|△≥0}=(﹣∞,﹣1]∪[2,+∞),
P={a|方程x2﹣2ax+(a+2)=0的两根都在[1,4]内}
记f(x)=x2﹣2ax+(a+2),且f(x)=0的两根都在[1,4]内
∴ ,
,
∴ ,
,
∴ ,
,
∴
∴实数a的取值范围为 .
.
∵A∩B≠
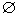 ,
, ∴方程x2﹣2ax+(a+2)=0有解,且至少有一解在区间(﹣∞,1)∪(4,+∞)内
直接求解情况比较多,考虑补集
设全集U={a|△≥0}=(﹣∞,﹣1]∪[2,+∞),
P={a|方程x2﹣2ax+(a+2)=0的两根都在[1,4]内}
记f(x)=x2﹣2ax+(a+2),且f(x)=0的两根都在[1,4]内
∴
 ,
,∴
 ,
,∴
 ,
,∴

∴实数a的取值范围为
 .
.
练习册系列答案
相关题目