题目内容
设常数a∈R,集合A={x|(x﹣1)(x﹣a)≥0},B={x|x≥a﹣1},若A∪B=R,则a的取值范围为( )
| A.(﹣∞,2) | B.(﹣∞,2] | C.(2,+∞) | D.[2,+∞) |
B
解析试题分析:当a>1时,A=(﹣∞,1]∪[a,+∞),B=[a﹣1,+∞),
若A∪B=R,则a﹣1≤1,
∴1<a≤2;
当a=1时,易得A=R,此时A∪B=R;
当a<1时,A=(﹣∞,a]∪[1,+∞),B=[a﹣1,+∞),
若A∪B=R,则a﹣1≤a,显然成立
∴a<1;
综上,a的取值范围是(﹣∞,2].
故选B.
考点:并集及其运算;一元二次不等式的解法
点评:此题考查了并集及其运算,二次不等式,以及不等式恒成立的条件,熟练掌握并集的定义是解本题的关键

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
设全集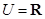 ,
,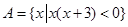 ,
,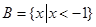 ,则图中阴影部分表示的集合为( )
,则图中阴影部分表示的集合为( )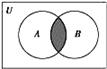
A.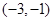 | B.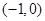 | C.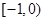 | D.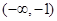 |
集合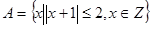 ,
,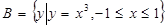 ,则
,则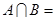 ( )
( )
A.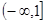 | B.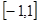 | C.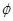 | D.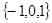 |
设集合 ,
, ,则
,则
A. | B. | C. | D. |
集合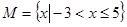 ,
,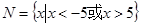 ,则
,则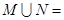 ( )
( )
A.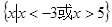 | B.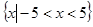 |
C.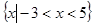 | D.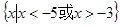 |
已知全集U=R,集合P={x|x2≤1},那么∁UP=( )
| A.(-∞,-1) | B.(1,+∞) |
| C.(-1,1) | D.(-∞,-1)∪(1,+∞) |
设集合 ,则
,则 =( )
=( )
A. | B. |
C. | D. |
设集合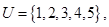 集合
集合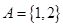 ,则
,则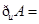 ( )
( )
A.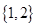 | B.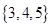 | C.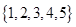 | D. |
 }关系的韦恩(Venn)图是
}关系的韦恩(Venn)图是