题目内容
(06年浙江卷文)对a,b![]() R,记max{a,b}=
R,记max{a,b}=![]() ,函数f(x)=max{|x+1|,|x-2|}(x
,函数f(x)=max{|x+1|,|x-2|}(x![]() R)的最小值是( )
R)的最小值是( )
(A)0 (B)![]() (C
(C ![]() (D)3
(D)3
答案:C
解析:当x<-1时,|x+1|=-x-1,|x-2|=2-x,因为(-x-1)-(2-x)=-3<0,所以
2-x>-x-1;当-1£x<![]() 时,|x+1|=x+1,|x-2|=2-x,因为(x+1)-(2-x)=2x-1<0,
时,|x+1|=x+1,|x-2|=2-x,因为(x+1)-(2-x)=2x-1<0,
x+1<2-x;当![]() £x<2时,x+1³2-x;当x³2时,|x+1|=x+1,|x-2|=x-2,显然x+1>x-2;
£x<2时,x+1³2-x;当x³2时,|x+1|=x+1,|x-2|=x-2,显然x+1>x-2;
故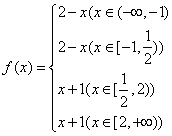 据此求得最小值为
据此求得最小值为![]() 。选C
。选C

练习册系列答案
相关题目