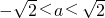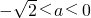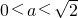题目内容
若a是实数,则关于x、y的方程组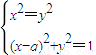 有四组不同实数解的一个充分非必要条件是( )
有四组不同实数解的一个充分非必要条件是( )A.
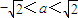
B.-1<a<1
C.
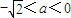
D.
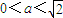
【答案】分析:先将关于x、y的方程组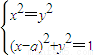 的实数解的问题转化为直线与圆的交点问题,当圆(x-a)2+y2=1与直线y=±x有四个交点时,-
的实数解的问题转化为直线与圆的交点问题,当圆(x-a)2+y2=1与直线y=±x有四个交点时,-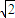 <a
<a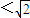 ,且a≠0.从而得出关于x、y的方程组
,且a≠0.从而得出关于x、y的方程组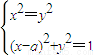 有四组不同实数解的一个充分必要条件,最后即可得出关于x、y的方程组
有四组不同实数解的一个充分必要条件,最后即可得出关于x、y的方程组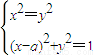 有四组不同实数解的一个充分非必要条件.
有四组不同实数解的一个充分非必要条件.
解答: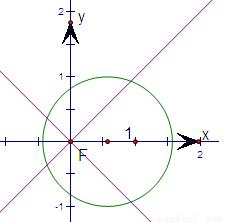 解:将关于x、y的方程组
解:将关于x、y的方程组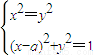 的实数解的问题转化为直线与圆的交点问题,
的实数解的问题转化为直线与圆的交点问题,
如图,
当圆(x-a)2+y2=1与直线y=±x有四个交点时,-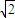 <a
<a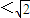 ,且a≠0.
,且a≠0.
即关于x、y的方程组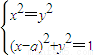 有四组不同实数解的一个充分必要条件是:,-
有四组不同实数解的一个充分必要条件是:,-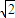 <a
<a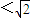 ,且a≠0.
,且a≠0.
则关于x、y的方程组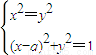 有四组不同实数解的一个充分非必要条件是:-1<a<1.
有四组不同实数解的一个充分非必要条件是:-1<a<1.
故选B.
点评:本小题主要考查根的存在性及根的个数判断、圆的方程等基础知识,考查数形结合思想、化归与转化思想.属于基础题.
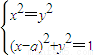 的实数解的问题转化为直线与圆的交点问题,当圆(x-a)2+y2=1与直线y=±x有四个交点时,-
的实数解的问题转化为直线与圆的交点问题,当圆(x-a)2+y2=1与直线y=±x有四个交点时,-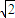 <a
<a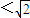 ,且a≠0.从而得出关于x、y的方程组
,且a≠0.从而得出关于x、y的方程组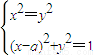 有四组不同实数解的一个充分必要条件,最后即可得出关于x、y的方程组
有四组不同实数解的一个充分必要条件,最后即可得出关于x、y的方程组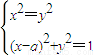 有四组不同实数解的一个充分非必要条件.
有四组不同实数解的一个充分非必要条件.解答:
 解:将关于x、y的方程组
解:将关于x、y的方程组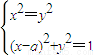 的实数解的问题转化为直线与圆的交点问题,
的实数解的问题转化为直线与圆的交点问题,如图,
当圆(x-a)2+y2=1与直线y=±x有四个交点时,-
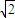 <a
<a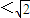 ,且a≠0.
,且a≠0.即关于x、y的方程组
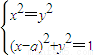 有四组不同实数解的一个充分必要条件是:,-
有四组不同实数解的一个充分必要条件是:,-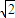 <a
<a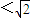 ,且a≠0.
,且a≠0.则关于x、y的方程组
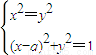 有四组不同实数解的一个充分非必要条件是:-1<a<1.
有四组不同实数解的一个充分非必要条件是:-1<a<1.故选B.
点评:本小题主要考查根的存在性及根的个数判断、圆的方程等基础知识,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
若a是实数,则关于x、y的方程组
有四组不同实数解的一个充分非必要条件是( )
|
A、-
| ||||
| B、-1<a<1 | ||||
C、-
| ||||
D、0<a<
|
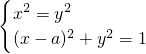 有四组不同实数解的一个充分非必要条件是
有四组不同实数解的一个充分非必要条件是