题目内容
随机变量 的分布列为
的分布列为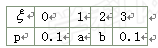
且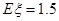 ,则
,则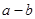 的值为 ( )
的值为 ( )
| A. -0.2 | B.0.2 | C.0.4 | D.0 |
B
解析考点:离散型随机变量的期望与方差.
专题:计算题.
分析:根据题意可得概率之和为1,即得a+b=0.8,又因为Eξ=0×0.1+1×a+2×b+3×0.1=1.6,进而可得a与b的数值,即可得到答案.
解答:解:由题意可得:0.1+a+b+0.1=1,
所以可得a+b=0.8①,
又因为Eξ=0×0.1+1×a+2×b+3×0.1=1.6,
所以可得a+2b=1.3②,
由①②解得a=0.3,b=0.5,
∴a-b=-0.2,
故应选B.
点评:解决此类问题的关键是熟练掌握离散型随机变量的分布列与其方差、均值之间的关系,此类问题一般出现在选择题中.

练习册系列答案
相关题目
已知随机变量ξ的分布列为且设η=2ξ+1,则η的期望值是( )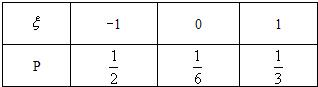

| A、1 | ||
B、
| ||
C、
| ||
D、-
|
已知随机变量ξ的分布列为且η=2ξ+3,则Eη等于( )
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
 的分布列为
的分布列为
 ,则
,则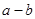 的值为
( )
的值为
( )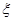 的分布列为且
的分布列为且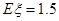 ,则
,则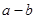 的值为 (
)
的值为 (
) 