Question

（文）已知，边AB上一点P₁，这里P₁异于A、B．由P₁引边OB的垂线P₁Q₁，Q₁是垂足，再由Q₁引边OA的垂线Q₁R₁，R₁是垂足．又由R₁引边AB的垂线R₁P₂，P₂是垂足．同样的操作连续进行，得到点 P_n、Q_n、R_n（n∈N^*）．设 ＜t_n＜1），如图．
（1）．求的值；
（2）．某同学对上述已知条件的研究发现如下结论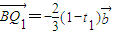：，问该同学这个结论是否正确？并说明理由；
（3）．当P₁、P₂重合时，求△P₁Q₁R₁的面积．

Answer 1

【答案】分析：（1）先求的平方的值，然后开根号即可；
（2）该同学的结论正确，利用余弦定理求出cos∠ABO，然后求出，而，即可知道结论：是否正确；
（3）根据向量的夹角公式求出cos∠BOA和cos∠BAO，从而求出 以及的值，当P₁、P₂重合时，有t₁=t₂，求出t₁的值，最后根据可求出面积．
解答：解：（1）因为-----（1分）
则 ；所以，--------------（4分）
（2）该同学的结论正确．-----------------------------------------（5分）
由（1）与已知，得，
由余弦定理  -----------------（6分）
又∵，则
则，所以，---------（8分）
（3）由已知得   -------------（9分）
（或用余弦定理求得，也可）∵，∴；
 =-------------------------（11分）
所以  ----------------------------------------------（12分）
当P₁、P₂重合时，有t₁=t₂，解得，---------------------------------（13分）
此时，∴，，，，
易求 ，，，-------------（17分）
故---------------------------（18分）
点评：本题主要考查了向量的数量积以及向量的夹角公式，同时考查了分析问题的能力，以及计算能力，属于中档题．