题目内容
【题目】将圆
上每一点的横坐标保持不变，纵坐标变为原来的2倍，得曲线C.
（1）写出C的参数方程；
（2）设直线
与C的交点为
，以坐标原点为极点，x轴正半轴为极坐标建立极坐标系，求过线段
的中点且与
垂直的直线的极坐标方程.
【答案】（1）
（t为参数）；（2）
.
【解析】
试题（1）设
为圆上的点，在曲线C上任意取一点（x，y），再根据
，由于点在圆
上，求出C的方程，化为参数方程．（2）解方程组求得
的坐标，可得线段
的中点坐标．再根据与l垂直的直线的斜率为
，用点斜式求得所求的直线的方程，再根据
可得所求的直线的极坐标方程．
（1）设为圆上的点，在已知变换下位C上点（x，y），依题意，得由
得
，即曲线C的方程为
.，故C得参数方程为（t为参数）.
（2）由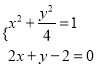
解得：
，或
.
不妨设
,则线段的中点坐标为
,所求直线的斜率为
，于是所求直线方程为
，
化极坐标方程，并整理得
，即.
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
