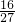题目内容
已知一个长方体交于一顶点的三条棱长之和为1,其表面积为
(1)将长方体的体积V表示为其中一条棱长x的函数关系,并写出定义域;
(2)求体积的最大、最小值;
(3)求体积最大时三棱长度.
【答案】分析:(1)根据一个长方体交于一顶点的三条棱长之和为1,其表面积为 ,设三条棱长分别为:x,y,z,则x+y+z=1,
,设三条棱长分别为:x,y,z,则x+y+z=1,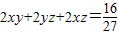 ,从而可得函数解析式,由此可确定函数的定义域;
,从而可得函数解析式,由此可确定函数的定义域;
(2)求导函数,求极值点,从而可确定函数的最值;
(3)由第(2)条件最大时x的值,结合x+y+z=1, ,可求三棱长度.
,可求三棱长度.
解答:解:(1)设三条棱长分别为:x,y,z,则x+y+z=1, …(1分)
…(1分)
得 ,
,
∴V=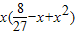 =
=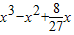 …(4分)
…(4分)
又∵y+z=1-x, ,
,
∴y、z是方程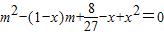 的两根
的两根 得
得 ≤x≤
≤x≤
∴V=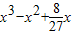 (
(  ≤x≤
≤x≤ ).…(6分)
).…(6分)
(2)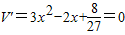 ,得
,得 或
或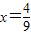 …(8分)
…(8分)
当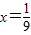 或
或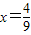 时,V有最小值
时,V有最小值 ,
,
当 或
或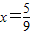 时,V有最大值
时,V有最大值 .…(10分)
.…(10分)
(3)当V有最大值时,三棱长分别为: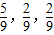 . …(12分)
. …(12分)
点评:本题i长方体为载体,考查函数关系的建立,考查导数的运用,考查函数的最值,有综合性.
 ,设三条棱长分别为:x,y,z,则x+y+z=1,
,设三条棱长分别为:x,y,z,则x+y+z=1,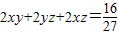 ,从而可得函数解析式,由此可确定函数的定义域;
,从而可得函数解析式,由此可确定函数的定义域;(2)求导函数,求极值点,从而可确定函数的最值;
(3)由第(2)条件最大时x的值,结合x+y+z=1,
 ,可求三棱长度.
,可求三棱长度.解答:解:(1)设三条棱长分别为:x,y,z,则x+y+z=1,
 …(1分)
…(1分)得
 ,
,∴V=
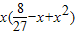 =
=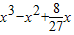 …(4分)
…(4分)又∵y+z=1-x,
 ,
,∴y、z是方程
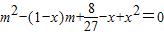 的两根
的两根 得
得 ≤x≤
≤x≤
∴V=
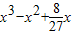 (
(  ≤x≤
≤x≤ ).…(6分)
).…(6分)(2)
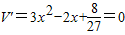 ,得
,得 或
或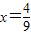 …(8分)
…(8分)当
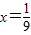 或
或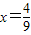 时,V有最小值
时,V有最小值 ,
,当
 或
或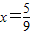 时,V有最大值
时,V有最大值 .…(10分)
.…(10分)(3)当V有最大值时,三棱长分别为:
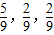 . …(12分)
. …(12分)点评:本题i长方体为载体,考查函数关系的建立,考查导数的运用,考查函数的最值,有综合性.

练习册系列答案
相关题目