题目内容
已知z为负数,且(1+3i)z为纯虚数,|z|=
.
(Ⅰ)求复数z;
(Ⅱ)若复数ω满足|2ω-z|≤1,求|ω|的最大值.
| 10 |
(Ⅰ)求复数z;
(Ⅱ)若复数ω满足|2ω-z|≤1,求|ω|的最大值.
分析:(Ⅰ)设出复数z,对复数方程求出z,通过复数的分子与分母同乘分母的共轭复数,化简复数通过复数的模求出复数z即可.(Ⅱ)设出复数ω,把复数z代入|2ω-z|≤1,求出复数满足方程,然后求|ω|的最大值.
解答:解:(Ⅰ)因为(1+3i)z为纯虚数,所以设(1+3i)z=ai,(a∈R,a≠0)
则为纯虚数,z=
=
=
;
∵|z|=
.
所以
=
,a=±10,
∴z=3+i或z=-3-i.
(Ⅱ)设ω=x+yi(x,y∈R),若z=3+i,则
|2ω-z|=|2x+2yi-3-i|=
≤1,
即(x-
)2+(y-
)2≤
,以(
,
)为圆心,
为半径的圆以及内部部分,
所求最大值就是圆心到原点的结论加上半径,
所以|ω|的最大值为
,
同理当z=-3-i时,|ω|的最大值为
.
则为纯虚数,z=
| ai |
| 1+3i |
| ai(1-3i) |
| (1+3i)(1-3i) |
| 3a+ai |
| 10 |
∵|z|=
| 10 |
所以
| ||
| 10 |
| 10 |
∴z=3+i或z=-3-i.
(Ⅱ)设ω=x+yi(x,y∈R),若z=3+i,则
|2ω-z|=|2x+2yi-3-i|=
| (2x-3)2+(2y-1)2 |
即(x-
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所求最大值就是圆心到原点的结论加上半径,
所以|ω|的最大值为
1+
| ||
| 2 |
同理当z=-3-i时,|ω|的最大值为
1+
| ||
| 2 |
点评:本题是中档题,考查复数的基本运算,复数的模的求法,复数满足的轨迹方程,考查转化思想,计算能力.

练习册系列答案
相关题目
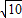 .
.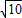 .
.