题目内容
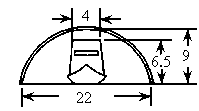
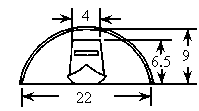
船行前方的河道上有一座圆拱桥，在正常水位时，拱圈最高点距水面为9 m，拱圈内水面宽22 m．船只在水面以上部分高6.5 m、船顶部宽4 m，故通行无阻．近日水位暴涨了2.7 m，船已经不能通过桥洞了．船员必须加重船载，降低船身．试问：船身必须降低多少，才能顺利地通过桥洞？
答案：
解析：
解析：
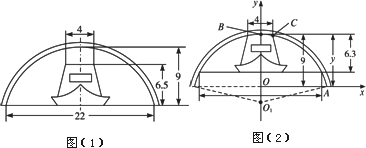
解：画出正常水位时的桥、船的示意图如图(1)；涨水后桥、船的示意图如图(2)．
以正常水位时河道中央为原点，建立如图(2)所示的坐标系．设桥拱圆顶的圆心在O1(x1，y1)，则x1＝0，因此桥拱圆顶在坐标系中的方程为x2＋(y－y1)2＝r2．其中r为桥拱半径．桥拱最高点B的坐标为(0，9)，桥拱与水线的交点A的坐标为(11，0)．圆O1过点A、B，因此?02＋(9－y1)2＝r2，112＋(0－y1)2＝r2，两式相减后得121＋18y1－81＝0，y1＝
≈－2.22；代回到两个方程之一，即可解出r≈11.22．所以桥拱圆顶的方程是x2＋(y＋2.22)2＝125.94．
当船行驶在河道的正中央时，船顶最宽处角点C的坐标为(x，y)，则x＝2．使船能通过桥洞的最低要求是点C正好的圆O1上，因此?C(2，y)应满足圆O1的方程，即22＋(y＋2.22)2＝125.94，解出y≈8.82．扣除水面上涨的2.70，点C距水面为8.82－2.70＝6.12．
因为船身在水面以上部分原高6.5，所以为使船能通过桥洞，必须降低船身6.5－6.12＝0.38(m)以上．
练习册系列答案
相关题目
