题目内容
如果实系数a1、b1、c1和a2、b2、c2都是非零常数.
(1)设不等式a1x2+b1x+c1>0和a2x2+b2x+c2>0的解集分别是A、B,试问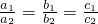 是A=B的什么条件?并说明理由.
是A=B的什么条件?并说明理由.
(2)在实数集中,方程a1x2+b1x+c1=0和a2x2+b2x+c2=0的解集分别为A和B,试问 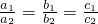 是A=B的什么条件?并说明理由.
是A=B的什么条件?并说明理由.
(3)在复数集中,方程a1x2+b1x+c1=0和a2x2+b2x+c2=0的解集分别为A和B,证明: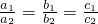 是A=B的充要条件.
是A=B的充要条件.
解:(1)若 a=b=c=1,a1=b1=c1=-1,则A≠B …(2分)
若 A=B=Φ,则两个不等式的系数之间没有关系. …(4分)
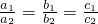 是A=B的既不充分也不必要条件. …(6分)
是A=B的既不充分也不必要条件. …(6分)
(2)若 A=B=Φ,则两个方程的系数之间没有关系. …(8分)
由于两个方程的系数对应成比例,所以两个方程式同解方程.…(10分
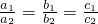 是A=B的充分也不必要条件 …(12分)
是A=B的充分也不必要条件 …(12分)
(3)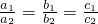 是A=B的充要条件 …(14分)
是A=B的充要条件 …(14分)
由于两个方程的系数对应成比例,所以两个方程是同解方程.充分性得证.…(16分)
由韦达定理可以证明必要性.…(18分)
分析:(1)通过举反例判断出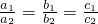 推不出A=B,反之A=B也推不出
推不出A=B,反之A=B也推不出 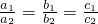 ,根据充要条件的有关定义得到结论.
,根据充要条件的有关定义得到结论.
(2)通过举反例判断出 A=B,推不出两个方程的系数之间有关系,反之当两个方程的系数对应成比例,两个方程式同解方程,利用充要条件的有关定义得到结结论.
(3)两个方程的系数对应成比例,所以两个方程是同解方程.充分性得证;由韦达定理可以证明必要性.
点评:本题考查判断应该命题是另一个命题的什么条件,应该两边互推,然后利用充要条件的有关定义加以判断;考查二次不等式,二次方程的解法.
若 A=B=Φ,则两个不等式的系数之间没有关系. …(4分)
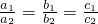 是A=B的既不充分也不必要条件. …(6分)
是A=B的既不充分也不必要条件. …(6分)(2)若 A=B=Φ,则两个方程的系数之间没有关系. …(8分)
由于两个方程的系数对应成比例,所以两个方程式同解方程.…(10分
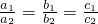 是A=B的充分也不必要条件 …(12分)
是A=B的充分也不必要条件 …(12分)(3)
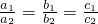 是A=B的充要条件 …(14分)
是A=B的充要条件 …(14分)由于两个方程的系数对应成比例,所以两个方程是同解方程.充分性得证.…(16分)
由韦达定理可以证明必要性.…(18分)
分析:(1)通过举反例判断出
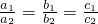 推不出A=B,反之A=B也推不出
推不出A=B,反之A=B也推不出 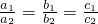 ,根据充要条件的有关定义得到结论.
,根据充要条件的有关定义得到结论.(2)通过举反例判断出 A=B,推不出两个方程的系数之间有关系,反之当两个方程的系数对应成比例,两个方程式同解方程,利用充要条件的有关定义得到结结论.
(3)两个方程的系数对应成比例,所以两个方程是同解方程.充分性得证;由韦达定理可以证明必要性.
点评:本题考查判断应该命题是另一个命题的什么条件,应该两边互推,然后利用充要条件的有关定义加以判断;考查二次不等式,二次方程的解法.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
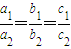 是A=B的什么条件?并说明理由.
是A=B的什么条件?并说明理由.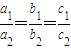 是A=B的什么条件?并说明理由.
是A=B的什么条件?并说明理由.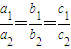 是A=B的充要条件.
是A=B的充要条件.