题目内容
凸多边形各内角度数成等差数列,最小角为120°,公差为5°,则边数n等于( )A.16
B.9
C.16或9
D.12
【答案】分析:先设出凸多边形的边数为n,凸多边形各内角度数成等差数列,最小角为120°,公差为5°,表示出等差数列的前n项和,再写出多边形的内角和,得到方程,解方程或代入选项进行检验.
解答:解:设出凸多边形的边数为n,
∵凸多边形各内角度数成等差数列,最小角为120°,公差为5°
∴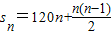 ×5°=180(n-2)
×5°=180(n-2)
整理可得n2-25n+144=0,
解可得n=16或9,
故选C.
点评:本题考查等差数列的前n项和,本题解题的关键是根据题意和多边形的内角和得到关于n的方程,本题是一个基础题.
解答:解:设出凸多边形的边数为n,
∵凸多边形各内角度数成等差数列,最小角为120°,公差为5°
∴
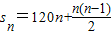 ×5°=180(n-2)
×5°=180(n-2)整理可得n2-25n+144=0,
解可得n=16或9,
故选C.
点评:本题考查等差数列的前n项和,本题解题的关键是根据题意和多边形的内角和得到关于n的方程,本题是一个基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
凸多边形各内角度数成等差数列,最小角为120°,公差为5°,则边数n等于( )
| A、16 | B、9 | C、16或9 | D、12 |