题目内容
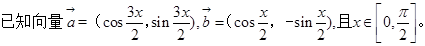
(1)求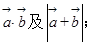
(2)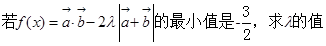 .
.
(1)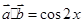 ;
;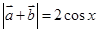 . (2)
. (2)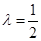 .
.
解析试题分析:(1)直接由向量的运算法则即可得.
(2)将(1)小题的结果代入得: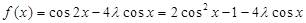 .这是一个关于
.这是一个关于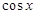 的二次式,所以通过配方利用二次函数的图象来求其最小值.
的二次式,所以通过配方利用二次函数的图象来求其最小值.
将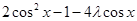 配方得
配方得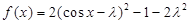 .
.  ,所以
,所以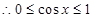 .
.
令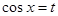 ,作出抛物线
,作出抛物线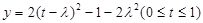 ,它的对称轴为
,它的对称轴为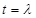 ,结合图象可知,需分
,结合图象可知,需分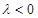 、
、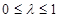 、
、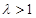 三种情况讨论.
三种情况讨论.
试题解析:(1)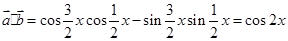 .
.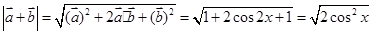 .
. ,所以
,所以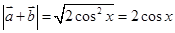 .
.
(2)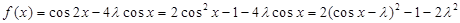 .
. ,所以
,所以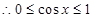 .
.
①当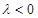 时,当且仅当
时,当且仅当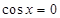 时,
时, 取最小值 1,这与题设矛盾.
取最小值 1,这与题设矛盾.
②当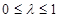 时,当且仅当
时,当且仅当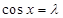 时,
时, 取最小值
取最小值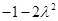 .由
.由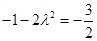 得
得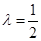 .
.
③当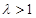 时,当且仅当
时,当且仅当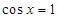 时,
时, 取最小值
取最小值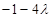 .由
.由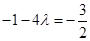 得
得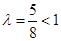 ,故舍去..
,故舍去..
综上得: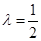 .
.
考点:1、向量的模及数量积;2、三角恒等变换;3、函数的最值.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
设向量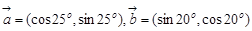 ,若
,若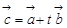 (tÎR),则
(tÎR),则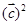 的最小值为
的最小值为
A. | B.1 | C.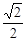 | D.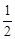 |
若向量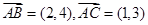 ,则
,则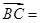 ( )
( )
| A.(1,1) | B.(-1,-1) | C.(3,7) | D.(-3,-7) |
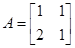 ,向量
,向量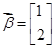 ,求向量
,求向量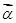 ,使得
,使得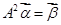
 中,
中, ,
, 为斜边
为斜边 上靠近顶点
上靠近顶点 的三等分点.
的三等分点. ,求
,求 ;
; ,求
,求 方向上的投影.
方向上的投影.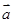 =(2,-1),
=(2,-1),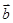 =(1,1),
=(1,1), =(-5,1),若
=(-5,1),若 ∥
∥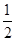
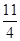
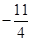
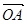 =
=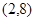 ,
,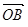 =
=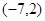 ,则
,则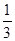
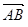 =_________
=_________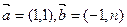 ,若
,若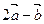 与
与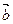 共线,则
共线,则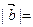 。
。 AC;在AB上取一点M,使得AM=
AC;在AB上取一点M,使得AM= BN;在CM的延长线上取点Q,使得
BN;在CM的延长线上取点Q,使得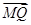 =λ
=λ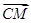 时,
时,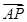 =
=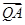 ,试确定λ的值.
,试确定λ的值.