题目内容
在边长为5的菱形ABCD中,AC=8.现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为| 9 | 25 |
(I)求证:平面ABD⊥平面CBD;
(II)若M是AB的中点,求折起后AC与平面MCD所成角的一个三角函数值.
分析:(I)由已知中边长为5的菱形ABCD中,AC=8.结合棱形的几何性质,我们易得到AO⊥OC,又AO⊥BD,结合线在垂直的判定定理及面面垂直的判定定理,即可得到答案.
(II)分别以OA,OC,OD所在直线为坐标轴建系,结合M是AB的中点,我们求出几何体中各顶点的坐标,进而求出直线AC的方向向量和平面MCD的法向量,代入向量夹角公式即可得到答案.
(II)分别以OA,OC,OD所在直线为坐标轴建系,结合M是AB的中点,我们求出几何体中各顶点的坐标,进而求出直线AC的方向向量和平面MCD的法向量,代入向量夹角公式即可得到答案.
解答: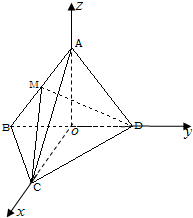 解:(Ⅰ)证明:菱形ABCD中,记AC,BD交点为O,AD=5,∴OA=4,OD=3
解:(Ⅰ)证明:菱形ABCD中,记AC,BD交点为O,AD=5,∴OA=4,OD=3
翻折后变成三棱椎A-BCD,在△ACD中,
AC2=AD2+CD2-2AD•CD•cos∠ADC
=25+25-2×5×5×
=32
在△AOC中,OA2+OC2=32=AC2,
∴∠AOC=90°,即AO⊥OC,又AO⊥BD,OC∩BD=O,
∴AO⊥平面BCD,(4分)
又AO?平面ABD,∴平面ABD⊥平面CBD.
(Ⅱ)由(Ⅰ)知OA,OC,OD两两互相垂直,分别以OA,OC,OD所在直线为坐标轴建系,
则A(0,0,4),B(0,-3,0),C(4,0,0),D(0,3,0),
M(0,-
,2),
=(4,
,-2),
=(4,-3,0),
=(4,0,-4),(8分)
设平面MCD的一个法向量为
=(x,y,z),则由
,得
,(10分)
令y=4,有
=(3,4,9)(10分)
设AC与平面MCD所成角为θ,sinθ=|cos?
>|=|
|=
∴AC与平面MCD所成角的正弦值为
,(12分)
 解:(Ⅰ)证明:菱形ABCD中,记AC,BD交点为O,AD=5,∴OA=4,OD=3
解:(Ⅰ)证明:菱形ABCD中,记AC,BD交点为O,AD=5,∴OA=4,OD=3翻折后变成三棱椎A-BCD,在△ACD中,
AC2=AD2+CD2-2AD•CD•cos∠ADC
=25+25-2×5×5×
| 9 |
| 25 |
在△AOC中,OA2+OC2=32=AC2,
∴∠AOC=90°,即AO⊥OC,又AO⊥BD,OC∩BD=O,
∴AO⊥平面BCD,(4分)
又AO?平面ABD,∴平面ABD⊥平面CBD.
(Ⅱ)由(Ⅰ)知OA,OC,OD两两互相垂直,分别以OA,OC,OD所在直线为坐标轴建系,
则A(0,0,4),B(0,-3,0),C(4,0,0),D(0,3,0),
M(0,-
| 3 |
| 2 |
| MC |
| 3 |
| 2 |
| DC |
| AC |
设平面MCD的一个法向量为
| n |
|
|
令y=4,有
| n |
设AC与平面MCD所成角为θ,sinθ=|cos?
| AC, |
| n |
| 12-36 | ||||
|
| 3 |
| 53 |
| 53 |
∴AC与平面MCD所成角的正弦值为
| 3 |
| 53 |
| 53 |
点评:本题考查的知识是平面与平面垂直的判定,用空间向量求直线与平面的夹角,其中选择恰当的原点建立坐标系,将线面夹角问题转化为向量夹角问题是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

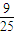 .
.