题目内容
已知函数 是
是 上的偶函数,若对于
上的偶函数,若对于 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 =____________.
=____________.
1
解析试题分析:由题意可知函数 的周期
的周期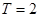 ,于是
,于是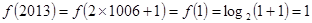 ,又函数
,又函数 是
是 上的偶函数,所以
上的偶函数,所以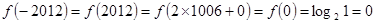 ,则
,则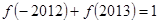 .
.
考点:周期函数、奇偶性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
已知函数 是
是 上的偶函数,若对于
上的偶函数,若对于 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 =____________.
=____________.
1
解析试题分析:由题意可知函数 的周期
的周期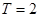 ,于是
,于是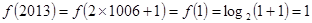 ,又函数
,又函数 是
是 上的偶函数,所以
上的偶函数,所以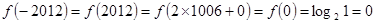 ,则
,则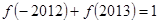 .
.
考点:周期函数、奇偶性.

 名校课堂系列答案
名校课堂系列答案