题目内容
已知棱长为4的正方体和其内切球O,质点P能均匀地落在正方体的任何位置,求质点P落在其内切球内的概率.
分析:质点P落在其内切球内的概率p=
,由此能求出结果.
| V球O |
| V正方体 |
解答:解:∵正方体的棱长为4,
∴其内切球O的半径R=2,
∵质点P能均匀地落在正方体的任何位置,
∴质点P落在其内切球内的概率
p=
=
=
.
故质点P落在其内切球内的概率为
.
∴其内切球O的半径R=2,
∵质点P能均匀地落在正方体的任何位置,
∴质点P落在其内切球内的概率
p=
| V球O |
| V正方体 |
| ||
| 43 |
| π |
| 6 |
故质点P落在其内切球内的概率为
| π |
| 6 |
点评:本题考查根据的求法,是基础题.解题时要认真审题,注意球的体积的运算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
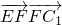 ;
;