题目内容
定义在(-∞,0)∪(0,+∞)上的奇函数f(x)在(0,+∞)上为增函数,当x>0时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]<0的解集是( )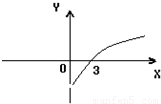
A.(-∞,-3)∪(0,3)
B.(-∞,-3)∪(3,+∞)
C.(-3,0)∪(3,+∞)
D.(-3,0)∪(0,3)
【答案】分析:不等式x[f(x)-f(-x)]<0等价于不等式xf(x)<0,再利用奇函数f(x)在(0,+∞)上为增函数,f(3)=0,可得f(x)在(-∞,0)上为增函数,f(-3)=0,由此可解不等式.
解答:解:由题意,不等式x[f(x)-f(-x)]<0等价于不等式xf(x)<0
∵奇函数f(x)在(0,+∞)上为增函数,f(3)=0
∴f(x)在(-∞,0)上为增函数,f(-3)=0
∴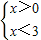 或
或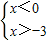
∴0<x<3或-3<x<0
故选D.
点评:本题考查函数单调性与奇偶性的结合,考查学生分析解决问题的能力,考查计算能力,属于中档题.
解答:解:由题意,不等式x[f(x)-f(-x)]<0等价于不等式xf(x)<0
∵奇函数f(x)在(0,+∞)上为增函数,f(3)=0
∴f(x)在(-∞,0)上为增函数,f(-3)=0
∴
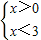 或
或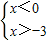
∴0<x<3或-3<x<0
故选D.
点评:本题考查函数单调性与奇偶性的结合,考查学生分析解决问题的能力,考查计算能力,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
若定义在(-1,0)内的函数f(x)=log2a(x+1)>0,则a的取值范围是( )
A、(0,
| ||
B、(0,
| ||
C、(
| ||
| D、(0,+∞) |