题目内容
(本大题满分13分)设函数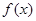 是定义域在
是定义域在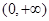 上的单调函数,且对于任意正数
上的单调函数,且对于任意正数 有
有 ,已知
,已知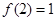 .
.
(1)求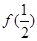 的值;
的值;
(2)一个各项均为正数的数列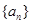 满足:
满足: ,其中
,其中 是数列
是数列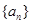 的前n项的和,求数列
的前n项的和,求数列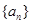 的通项公式;
的通项公式;
(3)在(2)的条件下,是否存在正数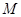 ,使
,使
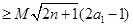
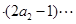
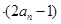 对一切
对一切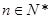 成立?若存在,求出M的取值范围;若不存在,说明理由.
成立?若存在,求出M的取值范围;若不存在,说明理由.
【答案】
(1)-1;
(2) ;
;
(3)存在正数 ,使所给定的不等式恒成立,
,使所给定的不等式恒成立, 的取值范围为
的取值范围为
【解析】(1)∵ ,令
,令 ,有
,有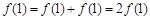 ,∴
,∴ .
.
再令 ,有
,有 ,∴
,∴ ,∴
,∴ …4分
…4分
(2)∵
 ,
,
又∵ 是定义域
是定义域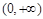 上单调函数,∵
上单调函数,∵ ,
,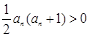 ,
,
∴ ……①
……①
当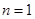 时,由
时,由 ,得
,得 ,当
,当 时,
时, ……②
……②
由①-②,得 ,
,
化简,得  ,∴
,∴ ,
,
∵ ,∴
,∴ ,即
,即 ,∴数列
,∴数列 为等差数列.
为等差数列.  ,公差
,公差 .
.
∴ ,故
,故 . ………… 8分
. ………… 8分
(3)∵ ,
,
令 =
= ,
,
而 .
.
∴
 =
= ,
,
∴ ,数列
,数列 为单调递增函数,由题意
为单调递增函数,由题意 恒成立,则只需
恒成立,则只需 =
= ,
,
∴ 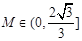 ,存在正数
,存在正数 ,使所给定的不等式恒成立,
,使所给定的不等式恒成立, 的取值范围为
的取值范围为 .
.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 (1)当圆柱底面半径
(1)当圆柱底面半径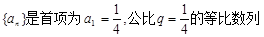 ,设
,设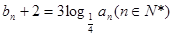 ,数列
,数列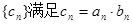 .
. 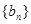 是等差数列;
是等差数列; 的前n项和Sn;
的前n项和Sn;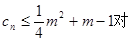 一切正整数n恒成立,求实数m的取值范围.
一切正整数n恒成立,求实数m的取值范围. 的扇形铁皮
的扇形铁皮 ,欲从其中裁剪出一块内接五边形
,欲从其中裁剪出一块内接五边形 ,使点
,使点 在
在 弧上,点
弧上,点 分别在半径
分别在半径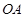 和
和 上,四边形
上,四边形 是矩形,点
是矩形,点 在弧
在弧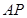 上,
上, 点在线段
点在线段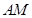 上,四边形
上,四边形 是直角梯形.现有如下裁剪方案:先使矩形
是直角梯形.现有如下裁剪方案:先使矩形 ,当矩形
,当矩形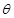 的值;
的值;
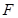 是椭圆
是椭圆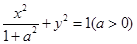 右焦点,点
右焦点,点 、
、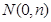 分别是x轴、 y上的动点,且满足
分别是x轴、 y上的动点,且满足 ,若点
,若点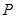 满足
满足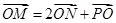 .
. 的方程;
的方程;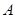 、
、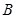 两点,直线
两点,直线 、
、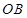 与直线
与直线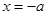 分别交于点
分别交于点 、
、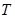 (其中
(其中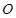 为坐标原点),试判断
为坐标原点),试判断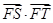 是否为定值?若是,求出这个定值;若不是,请说明理由.
是否为定值?若是,求出这个定值;若不是,请说明理由.