Question

(理)已知数列{a_n}中,a₁=t(t≠0且t≠1),a₂=t²,当x=t时,函数f(x)=(a_n-a_n-1)x²-(a_n+1-a_n)x(n≥2)取得极值.

(1)求证:数列{a_n+1-a_n}(n∈N^*)是等比数列;

(2)记b_n=a_nln|a_n|(n∈N^*),当t=时,数列{b_n}中是否存在最大项.若存在,是第几项?若不存在,请说明理由.

(文)已知等比数列{x_n}各项均为不等于1的正数,数列{y_n}满足=2(a＞0且a≠1),设y₃=18,y₆=12.

(1)求证:数列{y_n}是等差数列;

(2)若存在自然数M,使得n＞M时,x_n＞1恒成立,求M的最小值.

Answer 1

答案：(理)(1)证明:当x=t时,函数f(x)=(a_n-a_n-1)x²-(a_n+1-a_n)x(n≥2)取得极值,

∴t=,即数列{a_n+1-a_n}(n∈N^*)是等比数列.

(2)解:由(1)知a₂-a₁=t²-t,∴a_n=(a_n-a_n-1)+(a_n-1-a_n-2)+…+(a₂-a₁)+a₁=(tⁿ-t^n-1)+(t^n-1-t^n-2)+…+(t²-t)+t=tⁿ.

∴b_n=tⁿln｜tⁿ｜=ntⁿln｜t｜.

∵t=,∴b_n=n()ⁿ·ln.∴b_2k＜0,b_2k+1＞0(k∈N^*).

假设b_2k+1是数列{b_n}中的最大项,则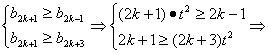

即≤k≤.

又∵k∈N^*,∴k=2,则b₅最大.

(文)(1)证明:∵y_n=2log_ax_n,∴y_n-y_n-1=2log_ax_n-2log_ax_n-1=2log_a.

又∵数列{x_n}为等比数列,∴2log_a为定值.∴{y_n}为等差数列.

(2)解:由(1)可得y_n=-2n+24,则x_n=a^-n+12,当a＞1时,a^-n+12＞a⁰,则n＜12,

∴不存在M∈N^*,使得n＞M时,x_n＞1恒成立;

当0＜a＜1时,a^-n+12＞a⁰,则n＞12.

∴取M=13,当n＞M时x_n＞1恒成立.∴M_min=13.