题目内容
下列四个命题中,假命题的个数是( )
(1)?x∈R,3x2+x≥-1;
(2)若事件A与B互为对立事件,P(A)=0.4,则P(B)=0.6;
(3)线性回归方程中的系数b,a是可正可负的;
(4)α∩β=l,则?直线a,a⊥α且a⊥β.
(1)?x∈R,3x2+x≥-1;
(2)若事件A与B互为对立事件,P(A)=0.4,则P(B)=0.6;
(3)线性回归方程中的系数b,a是可正可负的;
(4)α∩β=l,则?直线a,a⊥α且a⊥β.
分析:(1)由于△=1-12=-11<0,故3x2+x≥-1恒成立;
(2)若事件A与B互为对立事件,则P(A)+P(B)=1;
(3)线性回归方程中的系数b,a是可正可负的,显然正确;
(4)由于α∩β=l,则α,β不重合,故不存在直线a,a⊥α且a⊥β.
(2)若事件A与B互为对立事件,则P(A)+P(B)=1;
(3)线性回归方程中的系数b,a是可正可负的,显然正确;
(4)由于α∩β=l,则α,β不重合,故不存在直线a,a⊥α且a⊥β.
解答:解:(1)由于3x2+x≥-1?3x2+x+1≥0,△=1-12=-11<0,
故3x2+x≥-1恒成立,故(1)正确;
(2)若事件A与B互为对立事件,P(A)=0.4,
则P(B)=1-0.4=0.6,故(2)正确;
(3)线性回归方程中的系数b,a是可正可负的,故(3)正确;
(4)若α∩β=l,则α,β不重合,故不存在直线a,a⊥α且a⊥β,故(4)错误.
故答案为 B
故3x2+x≥-1恒成立,故(1)正确;
(2)若事件A与B互为对立事件,P(A)=0.4,
则P(B)=1-0.4=0.6,故(2)正确;
(3)线性回归方程中的系数b,a是可正可负的,故(3)正确;
(4)若α∩β=l,则α,β不重合,故不存在直线a,a⊥α且a⊥β,故(4)错误.
故答案为 B
点评:着重考查了不等式恒成立,对立事件概率和为1,面面垂直的性质定理和线面垂直的判定与性质等知识,属于基础题.

练习册系列答案
相关题目
 是等差数列
是等差数列 的前n项和,且
的前n项和,且 ,有下列四个命
,有下列四个命 ; B.在所有
; B.在所有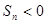 中,
中, 最大;
最大;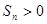 的
的 的个数有11个; D.
的个数有11个; D. ;
;