题目内容
若a>0, b>0, 且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( )
| A.2 | B.3 | C.6 | D.9 |
D
解析

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
已知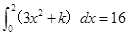 ,则
,则 ( )
( )
| A.1 | B.2 | C.3 | D.4 |
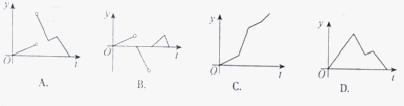
设函数f(x)在R上可导,其导函数为f/(x),且函数y=(1?x) f/(x)的图像如图所示,则下列结论中一定成立的是
| A.函数f(x)有极大值f(2)和极小值f(1) |
| B.函数f(x)有极大值f(?2)和极小值f(1) |
| C.函数f(x)有极大值f(2)和极小值f(?2) |
| D.函数f(x)有极大值f(?2)和极小值f(2) |
已知函数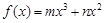 的图象在点
的图象在点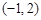 处的切线恰好与直线
处的切线恰好与直线 平行,若
平行,若 在区间
在区间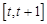 上单调递减,则实数
上单调递减,则实数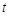 的取值范围是 ( )
的取值范围是 ( )
A.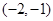 | B. | C.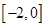 | D.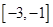 |
设 是定义在R上的奇函数,且
是定义在R上的奇函数,且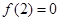 ,当x>0时,有
,当x>0时,有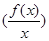 的导数小于零恒成立,则不等式
的导数小于零恒成立,则不等式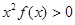 的解集是( )
的解集是( )
A.(一2,0) (2,+ (2,+ 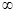 ) ) | B.(一2,0) (0,2) (0,2) |
C.(-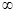 ,-2) ,-2) (2,+ (2,+ 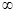 ) ) | D.(-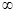 ,-2) ,-2) (0,2) (0,2) |
若函数 在其定义域内的一个子区间
在其定义域内的一个子区间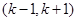 内不是单调函数,则实数
内不是单调函数,则实数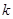 的取值范围是( )
的取值范围是( )
| A.[1,+∞) | B.[1,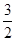 ) ) |
| C.[1,2) | D.[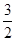 ,2) ,2) |
已知函数 在区间
在区间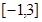 上是减函数,则
上是减函数,则 的最小值是( )
的最小值是( )
| A.1 | B.2 | C.3 | D.4 |
 的值是( )
的值是( ) B.
B. C.
C. D.
D.
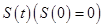 ,则导函数
,则导函数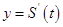 的图像大致 ( )
的图像大致 ( )