题目内容
已知函数f(x)=2sinxcosx+cos2x(x∈R).
(1)求f(x)的最小正周期和最大值;
(2)若θ为锐角,且f(θ+ )=
)=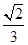 ,求tan2θ的值.
,求tan2θ的值.
(1) f(x)的最小正周期为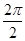 =π,最大值为.(2) tan2θ=
=π,最大值为.(2) tan2θ=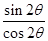 =2.
=2.
解析试题分析:利用二倍角公式以及两角和的正弦函数化简函数为一个角的一个三角函数的形式,
(Ⅰ)直接利用周期公式求出函数f (x)的最小正周期,最大值易求.
(Ⅱ)由f(θ+ )=
)=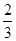 可得sin(2θ+
可得sin(2θ+ )=
)=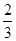 ,从而可得cos2θ=
,从而可得cos2θ=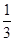 ,再注意研究0<2θ<π,进而可利用
,再注意研究0<2θ<π,进而可利用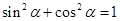 求出sin2θ,进而可求出tan2θ=
求出sin2θ,进而可求出tan2θ=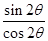 .
.
(1)f(x)=2sinxcosx+cos2x
=sin2x+cos2x
=(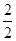 sin2x+
sin2x+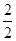 cos2x)
cos2x)
=sin(2x+ ).
).
∴f(x)的最小正周期为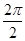 =π,最大值为.…………(6分)
=π,最大值为.…………(6分)
(2)∵f(θ+ )=
)=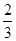 , ∴sin(2θ+
, ∴sin(2θ+ )=
)=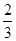 . ∴cos2θ=
. ∴cos2θ=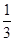 .
.
∵θ为锐角,即0<θ< ,∴0<2θ<π.
,∴0<2θ<π.
∴sin2θ=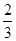 .
.
∴tan2θ=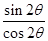 =2.…………(13分).
=2.…………(13分).
考点:倍角公式及两角和的正弦公式,正切公式,函数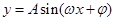 的性质,同角三角函数的基本关系式.
的性质,同角三角函数的基本关系式.
点评:本题主要是利用三角函数的二倍角公式,两角和的正弦公式,求解函数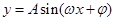 的最小正周期和最值,还考查了利用同角三角函数式求出其余名函数值,进而得到tan2θ的值.
的最小正周期和最值,还考查了利用同角三角函数式求出其余名函数值,进而得到tan2θ的值.

练习册系列答案
相关题目
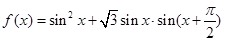 ,
,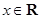
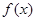 的最小正周期; (2)若
的最小正周期; (2)若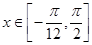 ,求函数
,求函数

 的最小正周期、单调增区间、对称轴和对称中心;
的最小正周期、单调增区间、对称轴和对称中心; 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到? 的最小正周期为
的最小正周期为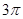 ,当
,当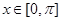 时,函数
时,函数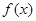 的最小值为0。
的最小值为0。 ,若
,若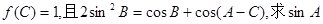 的值。
的值。 终边上一点
终边上一点 的坐标为
的坐标为 ,
, ;
; 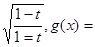
 ]
]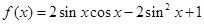
 的最小正周期和值域 (2)求
的最小正周期和值域 (2)求 ,且
,且 满足
满足
 的值.
的值. 的值.
的值. .
. 的最小正周期,并求其单调递增区间;
的最小正周期,并求其单调递增区间; 时,求
时,求