题目内容
关于函数 的四个结论:
的四个结论:
P1:函数 的最大值为
的最大值为 ;
;
P2:把函数 的图象向右平移
的图象向右平移 个单位后可得到函数
个单位后可得到函数 的图象;
的图象;
P3:函数 的单调递增区间为[
的单调递增区间为[ ],
], ;
;
P4:函数 图象的对称中心为(
图象的对称中心为( ),
), .其中正确的结论有( )
.其中正确的结论有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
B
解析试题分析:
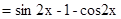
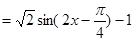 ,所以函数
,所以函数 的最大值为
的最大值为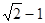 ,故P1错,易知P2错,
,故P1错,易知P2错,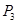 正确,
正确, 图象的对称中心为(
图象的对称中心为( ),
), .故P4正确,选B.
.故P4正确,选B.
考点:两角和与差的正弦函数;正弦函数的单调性.
点评:此题考查了两角和与差的正弦、正切函数公式,同角三角函数间的基本关系,余弦函数的奇偶性,正弦函数的单调性,以及三角函数图象的变换,熟练掌握公式是解本题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
函数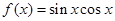 的最小正周期是( )
的最小正周期是( )
A. ? ? | B. ? ? | C. ? ? | D. |
已知ΔABC中,sinA= ,cosB=
,cosB= ,则cosC的值等于( )
,则cosC的值等于( )
A. 或 或 | B. | C. | D.- 或- 或- |
函数 的单调递增区间是 ( )
的单调递增区间是 ( )
A. | B. |
C. | D. |
已知扇形的半径为2,面积为4,则这个扇形圆心角的弧度数为
A. | B.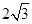 | C. | D.2 |
已知α为第二象限角,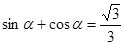 ,则cos2α=( )
,则cos2α=( )
A. | B. | C. | D. |
若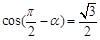 ,则
,则 ( ).
( ).
A. | B. | C. | D. |
函数 的值域为( ).
的值域为( ).
| A.[-2 ,2] | B.[- , , ] ] | C.[-1,1] | D.[- , ,  ] ] |
函数 是( )
是( )
A.奇函数且在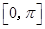 上单调递增 上单调递增 | B.奇函数且在 上单调递增 上单调递增 |
C.偶函数且在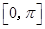 上单调递增 上单调递增 | D.偶函数且在 上单调递增 上单调递增 |