题目内容
已知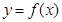 是奇函数,当
是奇函数,当 时,
时, ,且当
,且当 时,
时, 恒成立,则
恒成立,则 的最小值为 .
的最小值为 .
【答案】
9
【解析】解:因为 是奇函数,当
是奇函数,当 时,
时,

,且当 时,
时, 恒成立,
恒成立,
利用二次函数的性质可知函数的最大值和最小值与n,m的关系,然后得到 的最小值为9
的最小值为9

练习册系列答案
相关题目
 是奇函数,当
是奇函数,当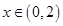 时,
时, ,当
,当 时,
时, 的最小值为1,则
的最小值为1,则 的值等于( )
的值等于( ) B.
B. C.
C. D.1
D.1 是奇函数,当
是奇函数,当 时,
时, 则
则 时,
时, ( )
( ) 是奇函数,当
是奇函数,当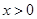 时,
时, ,且当
,且当 时,
时, 恒成立,则
恒成立,则 的最小值为
.
的最小值为
. 是奇函数,当
是奇函数,当 时,
时, 则
则 .
.