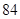题目内容
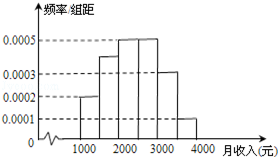
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在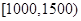 ,(单位:元).
,(单位:元).
(Ⅰ)估计居民月收入在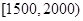 的概率;
的概率;
(Ⅱ)根据频率分布直方图估计样本数据的中位数;
(Ⅲ)若将频率视为概率,从本地随机抽取3位居民(看做有放回的抽样),求月收入在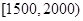 的居民数X的分布列和数学期望.
的居民数X的分布列和数学期望.
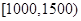 ,(单位:元).
,(单位:元).
(Ⅰ)估计居民月收入在
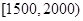 的概率;
的概率;(Ⅱ)根据频率分布直方图估计样本数据的中位数;
(Ⅲ)若将频率视为概率,从本地随机抽取3位居民(看做有放回的抽样),求月收入在
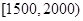 的居民数X的分布列和数学期望.
的居民数X的分布列和数学期望.(1)0.2;(2)2400;(3)分布列详见解析,0.9.
试题分析:(1)由频率分布直方图求概率;(2)利用频率分布直方图求中位数;(3)利用二项分布,求每一种情况的概率,列出分布列,求数学期望.
试题解析:(Ⅰ)由题意,居民月收入在
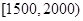 的概率约为
的概率约为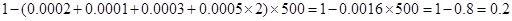 . 2分
. 2分(Ⅱ)由频率分布直方图知,中位数在
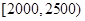 ,
,设中位数为
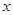 ,则
,则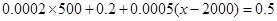 ,解得
,解得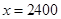 .6分
.6分(Ⅲ)居民月收入在
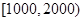 的概率为
的概率为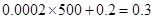 ,
, 由题意知,
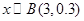 ,
,因此
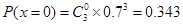 ,
,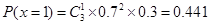 ,
,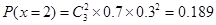 ,
,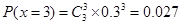 10分
10分故随机变量
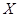 的分布列为
的分布列为| X | 0 | 1 | 2 | 3 |
| P | 0.343 | 0.441 | 0.189 | 0.027 |
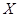 的数学期望为
的数学期望为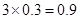 . 12分
. 12分
练习册系列答案
相关题目
 (单位:
(单位: )表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.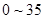





 年
年 月份的
月份的 天中随机抽取
天中随机抽取 天的
天的
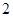 个,设
个,设 为空气质量类别为优或良的天数,求
为空气质量类别为优或良的天数,求


 ℃为低热,
℃为低热, ℃为中等热,
℃为中等热, ℃为高热。按此规定,记事件A为“从甲班发热的同学中任选两人,有中等热的同学”,记事件B为“从乙班发热的同学中任选两人,有中等热的同学”,分别求事件A和事件B的概率.
℃为高热。按此规定,记事件A为“从甲班发热的同学中任选两人,有中等热的同学”,记事件B为“从乙班发热的同学中任选两人,有中等热的同学”,分别求事件A和事件B的概率.
 名高三学生期中考试数学成绩的频率分布直方图如图所示,由图中数据估计此次数学成绩平均分为( )
名高三学生期中考试数学成绩的频率分布直方图如图所示,由图中数据估计此次数学成绩平均分为( )