题目内容
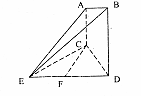
在直角梯形ABCD中,AB=2DC=2AD=2,∠DAB=∠ADC =90°,将△DBC沿BD向上折起,使面ABD垂直于面BDC,则C-DAB三棱锥的外接球的体积为________.
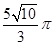
试题分析:设
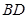 中点为
中点为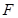 ,
,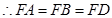 ,球心
,球心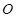 满足
满足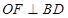 ,设
,设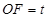 ,解三角形可知
,解三角形可知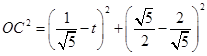 ,
,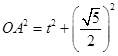
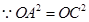
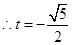
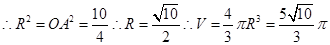
点评:要求球的体积,首先要求出半径,关键是找到球心的位置,依据球心到4个顶点距离相等及直角三角形斜边上的中线等于斜边的一般可确定下球心在过BD中点且垂直于平面ABD的直线上

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
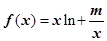 ,曲线
,曲线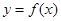 在
在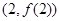 处的切线过点
处的切线过点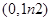 .
.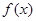 的解析式;
的解析式;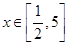 时,求
时,求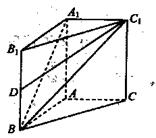
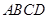 的对棱
的对棱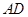 、
、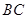 成
成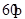 的角,且
的角,且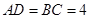 ,平行于
,平行于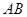 、
、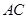 、
、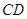 、
、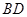 于
于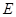 、
、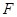 、
、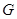 、
、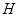 .
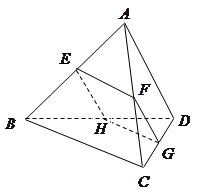
.
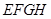 为平行四边形;
为平行四边形;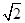 。
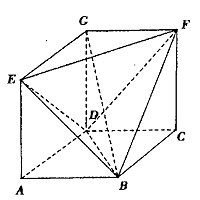
。
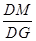 的值;若不存在,说明理由.
的值;若不存在,说明理由.