题目内容
 的内角
的内角 、
、 、
、 所对的边分别为
所对的边分别为 ,
, ,
, .若
.若 =2
=2 ,
, =1,
=1,  =2,则这样的三角形有 ( )
=2,则这样的三角形有 ( )
| A.只有一个 | B.有两个 | C.不存在 | D.无数个 |
C
解析试题分析:假设此三角形存在,由正弦定理可得 ,即
,即 ,解得
,解得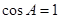 。因为角
。因为角 为三角形内角,
为三角形内角,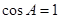 不成立,所以假设不成立。即此三角形不存在。故C正确。
不成立,所以假设不成立。即此三角形不存在。故C正确。
考点:正弦定理。

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
△ABC中,若 ,则△ABC的形状为( )
,则△ABC的形状为( )
| A.直角三角形 | B.等腰三角形 | C.等边三角形 | D.锐角三角形 |
在三角形ABC中,如果 ,那么A等于 ( )
,那么A等于 ( )
A. | B. | C. | D. |
△ABC中, 如果 , 那么△ABC是( )
, 那么△ABC是( )
| A.直角三角形 | B.等边三角形 |
| C.等腰直角三角形 | D.钝角三角形 |
在△ABC中,已知a=1、b=2,C=120°,则c=( )
| A.3 | B.4 | C.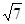 | D. |
在△ABC中,若 ,
, ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
在 中,
中, 则BC =( )
则BC =( )
A. | B. | C.2 | D. |
E,F是等腰直角 斜边AB上的三等分点,则tan
斜边AB上的三等分点,则tan ECF=( )
ECF=( )
A. | B. | C. | D. |
在△ABC中,内角A,B,C所对的边分别是 ,已知8b=5c,C=2B,则cosC=( )
,已知8b=5c,C=2B,则cosC=( )
A. |
B.- |
C.± |
D. |