题目内容
设 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当 时,
时, ,且
,且 ,则
,则 的解集是( )
的解集是( )
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0,3)
C.(-∞,-3)∪(3,+∞) D. (-∞,-3)∪(0,3)
【答案】
D
【解析】
试题分析: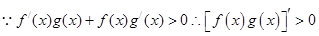 ,所以当
,所以当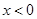 时函数
时函数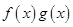 是增函数,
是增函数,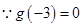
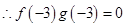
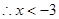 时
时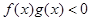 ,
,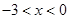 时
时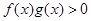 ,
,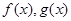 分别是定义在R上的奇函数和偶函数,所以
分别是定义在R上的奇函数和偶函数,所以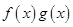 是R上的奇函数,所以当
是R上的奇函数,所以当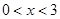 时
时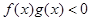 ,综上可知
,综上可知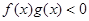 的解集为(-∞,-3)∪(0,3)
的解集为(-∞,-3)∪(0,3)
考点:利用函数性质解不等式
点评:本题首要是能够由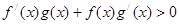 反用公式得到函数
反用公式得到函数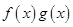 的单调性,进而结合图像的到
的单调性,进而结合图像的到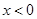 时的解集,借助于奇偶性得到R上的解集
时的解集,借助于奇偶性得到R上的解集

练习册系列答案
相关题目
 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当 时,
时, 且
且 则不等式
则不等式 的解集是
的解集是
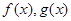 分别是定义在R上的奇函数和偶函数,
分别是定义在R上的奇函数和偶函数, 时,
时,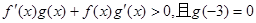 ,则不等式
,则不等式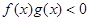 的解集是( )
的解集是( )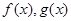 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当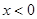 时,
时,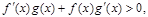 且
且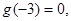 则不等式
则不等式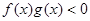 的解集是______________
的解集是______________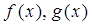 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当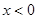 时,
时,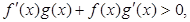 且
且 则不等式
则不等式 的解集是___________
的解集是___________