题目内容
三角形ABC中AP为BC边上的中线,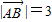 ,
,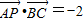 ,则
,则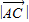 =( )
=( )A.2
B.3
C.

D.
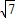
【答案】分析:由已知中三角形ABC中AP为BC边上的中线,根据向量加减法的三角形法则和平行四边形法则,可得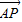 =
= (
(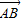 +
+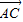 ),
),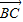 =
=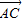 -
-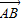 ,再由
,再由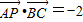 ,我们可以构造关于
,我们可以构造关于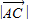 的方程,解方程即可得到答案.
的方程,解方程即可得到答案.
解答:解:∵AP为三角形ABC中BC边上的中线,
∴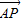 =
= (
(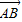 +
+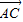 ),
),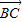 =
=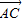 -
-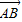 ,
,
∴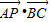 =
= (
(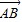 +
+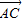 )•(
)•(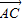 -
-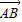 )=
)= (|
(|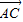 |2-|
|2-|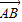 |2)=-2,
|2)=-2,
又∵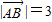 ,
,
∴|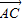 |2=5
|2=5
∴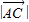 =
=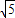
故选C
点评:本题考查的知识点是向量的模,平面向量数量积的运算,其中根据向量加减法的三角形法则和平行四边形法则,得到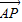 =
= (
(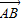 +
+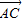 ),
),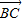 =
=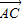 -
-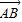 ,是解答本题的关键.
,是解答本题的关键.
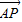 =
= (
(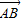 +
+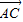 ),
),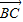 =
=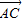 -
-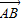 ,再由
,再由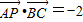 ,我们可以构造关于
,我们可以构造关于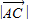 的方程,解方程即可得到答案.
的方程,解方程即可得到答案.解答:解:∵AP为三角形ABC中BC边上的中线,
∴
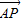 =
= (
(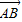 +
+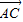 ),
),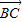 =
=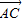 -
-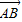 ,
,∴
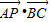 =
= (
(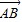 +
+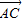 )•(
)•(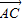 -
-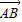 )=
)= (|
(|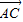 |2-|
|2-|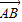 |2)=-2,
|2)=-2,又∵
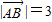 ,
,∴|
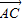 |2=5
|2=5∴
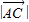 =
=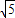
故选C
点评:本题考查的知识点是向量的模,平面向量数量积的运算,其中根据向量加减法的三角形法则和平行四边形法则,得到
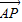 =
= (
(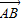 +
+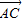 ),
),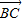 =
=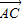 -
-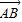 ,是解答本题的关键.
,是解答本题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
三角形ABC中AP为BC边上的中线,|
|=3,
•
=-2,则|
|=( )
| AB |
| AP |
| BC |
| AC |
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
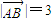 ,
,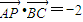 ,则
,则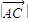 =( )
=( )
