题目内容
设数列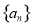 是集合
是集合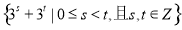 中所有的数从小到大排列成的数列,即
中所有的数从小到大排列成的数列,即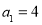 ,
,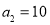 ,
, ,
,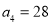 ,
,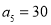 ,
, ,…,
,…,
将数列 中各项按照上小下大,左小右大的原则排成如下等腰直角三角形数表:
中各项按照上小下大,左小右大的原则排成如下等腰直角三角形数表:
4
10 12
28 30 36
…
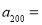 (用
(用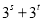 形式表示).
形式表示).
练习册系列答案
相关题目
题目内容
设数列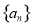 是集合
是集合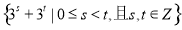 中所有的数从小到大排列成的数列,即
中所有的数从小到大排列成的数列,即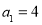 ,
,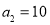 ,
, ,
,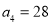 ,
,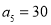 ,
, ,…,
,…,
将数列 中各项按照上小下大,左小右大的原则排成如下等腰直角三角形数表:
中各项按照上小下大,左小右大的原则排成如下等腰直角三角形数表:
4
10 12
28 30 36
…
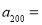 (用
(用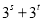 形式表示).
形式表示).