题目内容
已知三个不等式:① ;②
;② ;③
;③ ﹒要使同时满足①式和②的所有
﹒要使同时满足①式和②的所有 的值都满足③式,则实数
的值都满足③式,则实数 的取值范围是( )
的取值范围是( )
A. B.
B. C﹒
C﹒ D﹒
D﹒
C
解析试题分析:由①得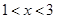 ,由②得
,由②得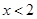 或
或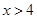 ,则同时满足①式和②式的所有
,则同时满足①式和②式的所有 的值为
的值为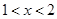 ,即③式不等式中
,即③式不等式中 的值至少包含区间
的值至少包含区间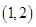 ,所以有
,所以有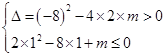 ,解得
,解得 .另解:将③式不等式化为
.另解:将③式不等式化为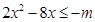 ,构造函数
,构造函数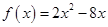 ,因为当
,因为当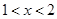 时,函数
时,函数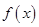 的值域为
的值域为 ,所以
,所以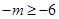 ,即
,即 .故正确答案为C.
.故正确答案为C.
考点:二次不等式

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知不等式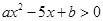 的解集为
的解集为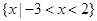 ,则不等式
,则不等式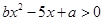 的解集为( )
的解集为( )
A.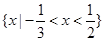 | B.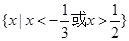 |
C.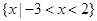 | D.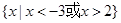 |
不等式 的解集是( )
的解集是( )
A. | B.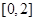 |
C.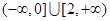 | D.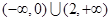 |
一元二次不等式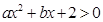 的解集是
的解集是 ,则
,则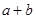 的值是( )。
的值是( )。
A.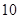 | B.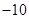 | C.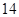 | D.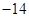 |
关于 的不等式kx2-kx+1>0解集为
的不等式kx2-kx+1>0解集为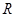 ,则k的取值范围是( )
,则k的取值范围是( )
| A.(0,+∞) | B.[0,+∞) | C.[0,4) | D.(0,4) |
不等式 的解集是( )
的解集是( )
A.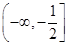 | B.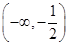 | C. | D. |
若函数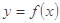 的导函数为
的导函数为 ,且
,且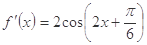 ,则
,则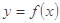 在
在 上的单调增区间为( )
上的单调增区间为( )
A. | B. |
C. 和 和 | D. 和 和 |
不等式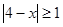 的解集为
的解集为
A. | B. | C. | D.R |
已知x∈(0,+∞)时,不等式9x-m·3x+m+1>0恒成立,则m的取值范围是( )
A.2-2 <m<2+2 <m<2+2 | B.m<2 |
C.m<2+2 | D.m≥2+2 |