题目内容
点P（x，y）在圆x2+y2=r2内，则直线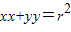
和已知圆的公共点的个数为（ ）A．0
B．1
C．2
D．不能确定
【答案】分析：先利用点到直线的距离，求得圆心到直线xx+yy=r2的距离，根据P在圆内，判断出 x2+y2＜r2，进而可知d＞r，故可知直线和圆相离．
解答：解：圆心O（0，0）到直线xx+yy=r2的距离为d=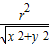
∵点M（x，y）在圆内，∴x2+y2＜r2，则有d＞r，
故直线和圆相离，直线与圆的公共点为0个
故选A．
点评：本题主要考查了直线与圆的位置关系．考查了数形结合的思想，直线与圆的位置关系的判定．解题的关键是看圆心到直线的距离与圆的半径的大小关系．
解答：解：圆心O（0，0）到直线xx+yy=r2的距离为d=
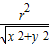
∵点M（x，y）在圆内，∴x2+y2＜r2，则有d＞r，
故直线和圆相离，直线与圆的公共点为0个
故选A．
点评：本题主要考查了直线与圆的位置关系．考查了数形结合的思想，直线与圆的位置关系的判定．解题的关键是看圆心到直线的距离与圆的半径的大小关系．
练习册系列答案
相关题目