题目内容
讨论函数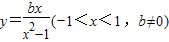
的单调性．
【答案】分析：先对函数y=f（x）进行求导，然后令导函数大于0（或小于0），求出x的范围，根据f′（x）＞0求得的区间是单调增区间，f′（x）＜0求得的区间是单调减区间，即可得到答案．
解答：解：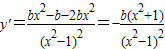
，
当b＞0时，y'＜0，函数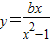
在（-1，1）上是减函数；
当b＜0时，y'＞0，函数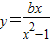
在（-1，1）上是增函数．
点评：本题主要考查导函数的正负与原函数的单调性之间的关系，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减．属于基础题．
解答：解：
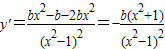，当b＞0时，y'＜0，函数
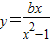在（-1，1）上是减函数；当b＜0时，y'＞0，函数
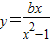在（-1，1）上是增函数．点评：本题主要考查导函数的正负与原函数的单调性之间的关系，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减．属于基础题．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目