题目内容
若 的最大值为m,且f(x)为偶函数,则m+u= .
的最大值为m,且f(x)为偶函数,则m+u= .
【答案】分析:由f(x)是偶函数可知f(-1)=f(1),代入可求u=0,所以f(x)=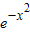 ,所以当x=0时函数f(x)取得最大值,从而可求所求.
,所以当x=0时函数f(x)取得最大值,从而可求所求.
解答:解:∵f(x)是偶函数,
∴f(-1)=f(1),
∴u=0
∴f(x)= ,
,
∴当x=0时函数f(x)取得最大值,且最大值为1,
∴m+μ=1.
故答案为:1.
点评:本题主要考查函数的奇偶性问题,另外涉及到指数函数的最值问题,这在考试中经常遇到,属于容易题.
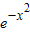 ,所以当x=0时函数f(x)取得最大值,从而可求所求.
,所以当x=0时函数f(x)取得最大值,从而可求所求.解答:解:∵f(x)是偶函数,
∴f(-1)=f(1),
∴u=0
∴f(x)=
 ,
,∴当x=0时函数f(x)取得最大值,且最大值为1,
∴m+μ=1.
故答案为:1.
点评:本题主要考查函数的奇偶性问题,另外涉及到指数函数的最值问题,这在考试中经常遇到,属于容易题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的最大值为m,且f(x)为偶函数,则m+u=________________.
的最大值为m,且f(x)为偶函数,则m+u=________________. 的最大值为m,且f(x)为偶函数,则m+u=______
的最大值为m,且f(x)为偶函数,则m+u=______ 的最大值为m,且f(x)为偶函数,则m+u= .
的最大值为m,且f(x)为偶函数,则m+u= . 的最大值为m,且f(x)为偶函数,则m+u= .
的最大值为m,且f(x)为偶函数,则m+u= .