题目内容
 (2012•开封二模)如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠DAB=60°.
(2012•开封二模)如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠DAB=60°.(1)证明:∠PBC=90°;
(2)若PB=3,求直线AB与平面PBC所成角的正弦值.
分析:(1)取AD中点O,连OP、OB,证明AD⊥平面POB,利用BC∥AD,可得BC⊥平面POB,从而可得结论;
(2)建立空间直角坐标系,求出平面PBC的法向量,利用向量的夹角公式,即可求直线AB与平面PBC所成角的正弦值.
(2)建立空间直角坐标系,求出平面PBC的法向量,利用向量的夹角公式,即可求直线AB与平面PBC所成角的正弦值.
解答: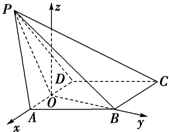 (1)证明:取AD中点O,连OP、OB,由已知得:OP⊥AD,OB⊥AD,
(1)证明:取AD中点O,连OP、OB,由已知得:OP⊥AD,OB⊥AD,
又OP∩OB=O,∴AD⊥平面POB,
∵BC∥AD,∴BC⊥平面POB,
∵PB?平面POB,∴BC⊥PB,即∠PBC=90°.
(2)解:如图,以O为坐标原点,建立空间直角坐标系O-xyz,则A(1,0,0),B(0,
,0),C(-1,
,0),
由PO=BO=
,PB=3,得∠POB=120°,∴∠POz=30°,∴P(0,-
,
),
则
=(-1,
,0),
=(-1,0,0),
=(0,
,-
),
设平面PBC的法向量为
=(x,y,z),则
,取z=
,则
=(0,1,
),
设直线AB与平面PBC所成的角为θ,则sinθ=|cos<
,
>|=
.
 (1)证明:取AD中点O,连OP、OB,由已知得:OP⊥AD,OB⊥AD,
(1)证明:取AD中点O,连OP、OB,由已知得:OP⊥AD,OB⊥AD,又OP∩OB=O,∴AD⊥平面POB,
∵BC∥AD,∴BC⊥平面POB,
∵PB?平面POB,∴BC⊥PB,即∠PBC=90°.
(2)解:如图,以O为坐标原点,建立空间直角坐标系O-xyz,则A(1,0,0),B(0,
| 3 |
| 3 |
由PO=BO=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
则
| AB |
| 3 |
| BC |
| PB |
3
| ||
| 2 |
| 3 |
| 2 |
设平面PBC的法向量为
| n |
|
| 3 |
| n |
| 3 |
设直线AB与平面PBC所成的角为θ,则sinθ=|cos<
| AB |
| n |
| ||
| 4 |
点评:本题考查直线与平面垂直,考查线面角,考查空间想象能力,逻辑推理能力,属于中档题.

练习册系列答案
相关题目
 (2012•开封二模)如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则
(2012•开封二模)如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°,则