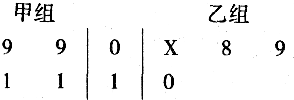题目内容
下面的茎叶图记录了甲、乙两组各四位同学在“学雷锋树新风”活动中植树的棵数,但乙组记录中有一个数据(用X表示)受污而无法确认.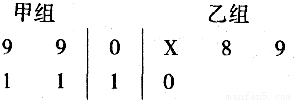
(1)若乙组同学植树棵数的平均数比甲组同学植树棵数的平均数少2,试确定受污的数X的值;
(2)在(1)的条件下,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
【答案】分析:(1)读出茎叶图的数据,利用平均数公式,方程思想求解即可.
(2)当X=5时,分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能,而这两名同学的植树总棵数为19的情况有 2+2=4种,由此求得两名同学的植树总棵数为19的概率.
解答:解:(1)由于甲组同学植树的平均数为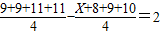 ,X=5…(2分)
,X=5…(2分)
(2)记甲组四名同学为A1,A2,A3,A4,他们植树的棵数依次为9,9,11,11;乙组四名同学为B1,B2,B3,B4,他们植树的棵数依次为5,8,9,10,分别从甲、乙两组中随机选取一名同学,所有可能的结果有16个,它们是:(A1B1),(A1B2),(A1B3),(A1B4)
(A2B1),(A2B2),(A2B3),(A2B4)(A3B1),(A3B2),(A3B3),(A3B4),(A4B1),(A4B2),(A4B3),(A4B4)
用C表示:“选出的两名同学的植树总棵数为19”这一事件,则C中的结果有4个,它们是:(A1B4),(A2B4),(A3B2),(A4B2)
,故所求概率为P(C)=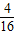 =
= …(12分)
…(12分)
(注:如果没有列出来,只要正确说明了各种情况也得相应的分值)
点评:本题主要考查古典概型及其概率计算公式的应用,茎叶图的应用,求一组数据的平均数和方差,属于基础题.
(2)当X=5时,分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能,而这两名同学的植树总棵数为19的情况有 2+2=4种,由此求得两名同学的植树总棵数为19的概率.
解答:解:(1)由于甲组同学植树的平均数为
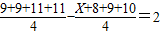 ,X=5…(2分)
,X=5…(2分)(2)记甲组四名同学为A1,A2,A3,A4,他们植树的棵数依次为9,9,11,11;乙组四名同学为B1,B2,B3,B4,他们植树的棵数依次为5,8,9,10,分别从甲、乙两组中随机选取一名同学,所有可能的结果有16个,它们是:(A1B1),(A1B2),(A1B3),(A1B4)
(A2B1),(A2B2),(A2B3),(A2B4)(A3B1),(A3B2),(A3B3),(A3B4),(A4B1),(A4B2),(A4B3),(A4B4)
用C表示:“选出的两名同学的植树总棵数为19”这一事件,则C中的结果有4个,它们是:(A1B4),(A2B4),(A3B2),(A4B2)
,故所求概率为P(C)=
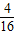 =
= …(12分)
…(12分)(注:如果没有列出来,只要正确说明了各种情况也得相应的分值)
点评:本题主要考查古典概型及其概率计算公式的应用,茎叶图的应用,求一组数据的平均数和方差,属于基础题.

练习册系列答案
相关题目