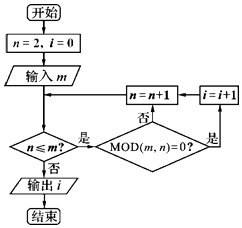
题目内容
【题目】如图,在平面直角坐标系xOy中,椭圆Ω: ![]() 的离心率为
的离心率为 ![]() ,直线l:y=2上的点和椭圆Ω上的点的距离的最小值为1.
,直线l:y=2上的点和椭圆Ω上的点的距离的最小值为1.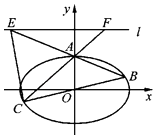
(Ⅰ) 求椭圆Ω的方程;
(Ⅱ) 已知椭圆Ω的上顶点为A,点B,C是Ω上的不同于A的两点,且点B,C关于原点对称,直线AB,AC分别交直线l于点E,F.记直线AC与AB的斜率分别为k1 , k2
①求证:k1k2为定值;
②求△CEF的面积的最小值.
【答案】解:(Ⅰ)由题知b=1,由 ![]() ,
,
所以a2=2,b2=1.
故椭圆的方程为 ![]() .
.
(Ⅱ)①证法一:设B(x0 , y0)(y0>0),则 ![]() ,
,
因为点B,C关于原点对称,则C(﹣x0 , ﹣y0),
所以 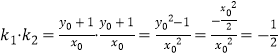 .
.
证法二:直线AC的方程为y=k1x+1,
由 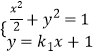 得
得 ![]() ,
,
解得 ![]() ,同理
,同理 ![]() ,
,
因为B,O,C三点共线,则由 ![]() ,
,
整理得(k1+k2)(2k1k2+1)=0,
所以 ![]() .
.
②直线AC的方程为y=k1x+1,直线AB的方程为y=k2x+1,不妨设k1>0,则k2<0,
令y=2,得 ![]() ,
,
而 ![]() ,
,
所以,△CEF的面积 ![]() =
= ![]()
= ![]() .
.
由 ![]() 得
得 ![]() ,
,
则S△CEF= ![]() ,当且仅当
,当且仅当 ![]() 取得等号,
取得等号,
所以△CEF的面积的最小值为 ![]()
【解析】(Ⅰ)由题知b=1,由 ![]() ,b=1,联立解出即可得出.(Ⅱ)①证法一:设B(x0 , y0)(y0>0),则
,b=1,联立解出即可得出.(Ⅱ)①证法一:设B(x0 , y0)(y0>0),则 ![]() ,因为点B,C关于原点对称,则C(﹣x0 , ﹣y0),利用斜率计算公式即可得出.证法二:直线AC的方程为y=k1x+1,与椭圆方程联立可得坐标,即可得出.②直线AC的方程为y=k1x+1,直线AB的方程为y=k2x+1,不妨设k1>0,则k2<0,令y=2,得
,因为点B,C关于原点对称,则C(﹣x0 , ﹣y0),利用斜率计算公式即可得出.证法二:直线AC的方程为y=k1x+1,与椭圆方程联立可得坐标,即可得出.②直线AC的方程为y=k1x+1,直线AB的方程为y=k2x+1,不妨设k1>0,则k2<0,令y=2,得 ![]() ,可得△CEF的面积
,可得△CEF的面积 ![]() .
.

练习册系列答案
相关题目