题目内容
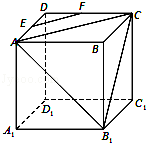
(4分)(2011•福建)如图,正方体ABCD﹣A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于 .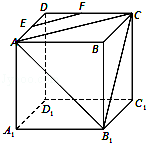

试题分析:根据已知EF∥平面AB1C和线面平行的性质定理,证明EF∥AC,又点E为AD的中点,点F在CD上,以及三角形中位线定理可知点F是CD的中点,从而求得线段EF的长度.
解:∵EF∥平面AB1C,EF⊆平面AC,平面AB1C∩平面AC=AC,
∴EF∥AC,
又点E为AD的中点,点F在CD上,
∴点F是CD的中点,
∴EF=
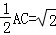 .
.故答案为
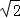 .
.
点评:此题是个基础题.考查线面平行的性质定理,同时考查学生对基础知识的记忆、理解和熟练应用的能力.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 圆柱
圆柱  圆锥
圆锥  四面体
四面体  三棱柱
三棱柱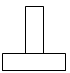
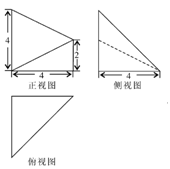
 ,则正视图中的
,则正视图中的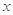 的值是( )
的值是( )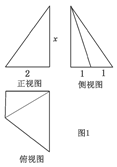




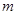 ,4的对面的数字为
,4的对面的数字为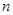 ,则
,则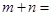 ( )
( )