题目内容
内接于半径为R的球且体积最大的圆柱体的高为__________.
解析：作轴截面如下图，设圆柱高为2h，则底面半径为
,圆柱体体积为V=π（R2-h2）·2h=2πR2h-2πh3,
令V′=0得：2πR2-6πh2=0,
∴h=
R.即当2h=
R时，圆柱体的体积最大.
答案：
R
练习册系列答案
相关题目
内接于半径为
R的球且体积最大的圆柱体的高为[
]|
A ． |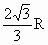
B ． |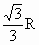
|
C ． |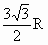
D ． |
题目内容
内接于半径为R的球且体积最大的圆柱体的高为__________.
解析：作轴截面如下图，设圆柱高为2h，则底面半径为,圆柱体体积为V=π（R2-h2）·2h=2πR2h-2πh3,
令V′=0得：2πR2-6πh2=0,
∴h=R.即当2h=R时，圆柱体的体积最大.
答案：R
内接于半径为
R的球且体积最大的圆柱体的高为[
]|
A ． |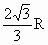
B ． |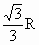
|
C ． |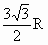
D ． |
R
R
R
R