题目内容
某幼儿园在“六·一儿童节”开展了一次亲子活动,此次活动由宝宝和父母之一(后面以家长代称)共同完成,幼儿园提供了两种游戏方案:
方案一 宝宝和家长同时各抛掷一枚质地均匀的正方体骰子(六个面的点数分别是1,2,3,4,5,6),宝宝所得点数记为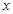 ,家长所得点数记为
,家长所得点数记为 ;
;
方案二 宝宝和家长同时按下自己手中一个计算器的按钮(此计算器只能产生区间[1,6]的随机实数),宝宝的计算器产生的随机实数记为 ,家长的计算器产生的随机实数记为
,家长的计算器产生的随机实数记为 .
.
(Ⅰ)在方案一中,若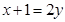 ,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率;
,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率;
(Ⅱ)在方案二中,若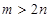 ,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率.
,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率.
【答案】
(Ⅰ)  ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:本题是一个概率问题.(Ⅰ)由题意可得符合条件的情况共有3种,而总共的事件有36种,所以可求得概率.本小题是古典概型的问题. (Ⅱ)由题意知m,n要满足的条件是一个不等式.并且m,n是连续的实数.所以让m,n分别为横轴和纵轴建立坐标系.而m,n所围成的正方形的面积是25.能中奖的条件满足的范围是所围成的面积是4.所以可求得符合条件的概率.本题的属于概率的应用,这类题型首要的是要读懂题意,明白在说些什么,表示那些数学知识.
试题解析:(Ⅰ)由题意可得,宝宝和家长所得点数x,y所有取值的基本事件总数为36.而满足x+1=2y的(x,y)有:(1,1),(3,2),(5,3)共3组.则抛掷一次后宝宝得小红花的概率 .
.
(Ⅱ)由题意m,n∈[1,6],则(m,n)所有值组成一个边长为5的正方形,其面积为25.(m,n)满足不等式m>2n,所占区域面积为 =4.则按下一次按钮后宝宝得兴趣读物一本的概率
=4.则按下一次按钮后宝宝得兴趣读物一本的概率 .
.
考点:1.古典概型;2.概率公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
随机调查某校50个学生在“六一”儿童节的午餐费,结果如下表:
这50个学生“六一”节午餐费的平均值和方差分别是( )
| 餐费(元) | 3 | 4 | 5 |
| 人数 | 10 | 20 | 20 |
| A、4.2,0.56 | ||
B、4.2,
| ||
| C、4,0.6 | ||
D、4,
|