题目内容
已知函数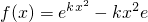 (k>0)(e为自然对数的底数)
(k>0)(e为自然对数的底数)
(1)求f(x)的极值
(2)对于数列{an},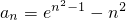 (n∈N*)
(n∈N*)
①证明:an<an+12
②考察关于正整数n的方程an=n是否有解,并说明理由.
解:(1)由f′(x)=2kx(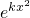 -e)=0得,x=0或x=±
-e)=0得,x=0或x=±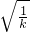 ,
,
∴f(x)在 (-∞,-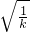 )单调递减,(-
)单调递减,(-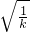 ,0)单调递增,(0,
,0)单调递增,(0,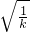 )单调递减,(
)单调递减,(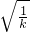 ,+∞)单调递增,
,+∞)单调递增,
∴f(x)极大=f(0)=1,f(x)极小值=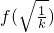 =0,
=0,
(2)①当k=1时,f(x)=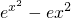 =
=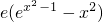 ,
,
由(1)知f(x)在(1,+∞)上递增,从而an<an+1
②由an=n,得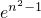 =n2+n,
=n2+n,
因n∈N+,得 n2-1是整数,所以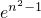 是无理数,
是无理数,
而n2+n为整数,所以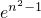 ≠n2+n
≠n2+n
即方程an=n无解
分析:(1)由f′(x)=0可求得x=0或x=±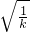 ,从而可求得其单调区间,继而可求得f(x)的极值;
,从而可求得其单调区间,继而可求得f(x)的极值;
(2)①观察得知,当k=1时,f(x)=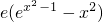 ,an=
,an=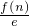 ,利用f(x)在(1,+∞)上递增,即可证得an<an+1;
,利用f(x)在(1,+∞)上递增,即可证得an<an+1;
(3)由an=n,得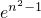 =n2+n,分析等号两端即可得到答案.
=n2+n,分析等号两端即可得到答案.
点评:本题考查利用导数研究函数的极值,着重考查利用导数研究函数的单调性,突出分类讨论思想与转化思想的综合运用,属于难题.
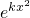 -e)=0得,x=0或x=±
-e)=0得,x=0或x=±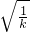 ,
,∴f(x)在 (-∞,-
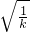 )单调递减,(-
)单调递减,(-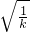 ,0)单调递增,(0,
,0)单调递增,(0,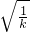 )单调递减,(
)单调递减,(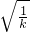 ,+∞)单调递增,
,+∞)单调递增,∴f(x)极大=f(0)=1,f(x)极小值=
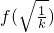 =0,
=0,(2)①当k=1时,f(x)=
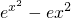 =
=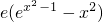 ,
,由(1)知f(x)在(1,+∞)上递增,从而an<an+1
②由an=n,得
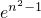 =n2+n,
=n2+n,因n∈N+,得 n2-1是整数,所以
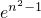 是无理数,
是无理数,而n2+n为整数,所以
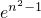 ≠n2+n
≠n2+n即方程an=n无解
分析:(1)由f′(x)=0可求得x=0或x=±
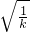 ,从而可求得其单调区间,继而可求得f(x)的极值;
,从而可求得其单调区间,继而可求得f(x)的极值;(2)①观察得知,当k=1时,f(x)=
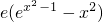 ,an=
,an=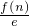 ,利用f(x)在(1,+∞)上递增,即可证得an<an+1;
,利用f(x)在(1,+∞)上递增,即可证得an<an+1;(3)由an=n,得
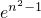 =n2+n,分析等号两端即可得到答案.
=n2+n,分析等号两端即可得到答案.点评:本题考查利用导数研究函数的极值,着重考查利用导数研究函数的单调性,突出分类讨论思想与转化思想的综合运用,属于难题.

练习册系列答案
相关题目
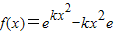 (k>0)(e为自然对数的底数)
(k>0)(e为自然对数的底数) (n∈N*)
(n∈N*)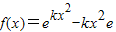 (k>0),求f(x)的极值.
(k>0),求f(x)的极值.