题目内容
在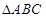 中,角
中,角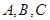 所对的边分别为
所对的边分别为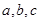 ,
,
 ,且
,且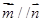 .求:
.求:
(1)求角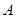 的值;
的值;
(2)求 的取值范围.
的取值范围.
【答案】
(1)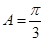 ;(2)
;(2)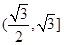
【解析】
试题分析:(1)由于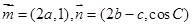 ,且
,且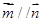 .根据向量的坐标形式平行的公式可得出一个关系式.再通过三角形中正弦定理将边转化化为角.即可得一个关于角A,B,C的三角函数的等式.然后利用
.根据向量的坐标形式平行的公式可得出一个关系式.再通过三角形中正弦定理将边转化化为角.即可得一个关于角A,B,C的三角函数的等式.然后利用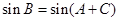 将三个角转化为两个角.从而可求得结论.
将三个角转化为两个角.从而可求得结论.
(2)由(1)可得∠A= .所以
.所以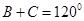 .利用这个关系将消去一个角,再利用角的和差公式展开,通过化简,再利用化一公式即可得到一个三角函数的式子.再根据角的范围求出取值范围.
.利用这个关系将消去一个角,再利用角的和差公式展开,通过化简,再利用化一公式即可得到一个三角函数的式子.再根据角的范围求出取值范围.
试题解析:(1)由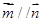 得:
得: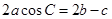 , 2分
, 2分
由正弦定理得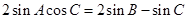
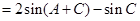

又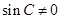
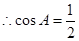 ,从而得
,从而得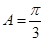 . 6分
. 6分
(2)由(1)知: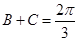 .
.
 …10分
…10分
又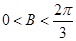 ,
,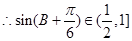
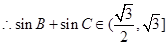 13
13
考点:1.向量的坐标形式的平行公式.2.三角形中互补角的相互转化.3.三角函数中的化一公式.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若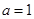 ,
,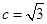 ,
,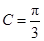 ,则
,则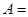 .
. 中,角
中,角 所对的边分别为
所对的边分别为 .向量
.向量 ,
, .已知
.已知 ,
, .
. 的大小;
的大小;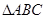 中,角
中,角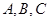 所对的边分别为
所对的边分别为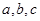 ,且满足
,且满足 ,
,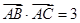 .
. 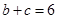 ,求
,求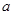 的值.
的值. 中,角
中,角 所对的边分别为
所对的边分别为 ,满足
,满足 ,且
,且 .
. 的值;
的值;
 ,求
,求 的值.
的值.