题目内容
（02年全国卷理）（12分）
如图，正方形
、
的边长都是1，而且平面、互相垂直。点
在
上移动，点
在
上移动，若
（
）
（1）求
的长；
（2）
为何值时，的长最小；
（3）当的长最小时，求面
与面
所成二面角
的大小。
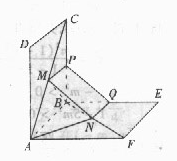
）解析：（I）作
∥
交
于点
，
∥交
于点
，连结
，依题意可得∥，且
，即
是平行四边形。
∴
由已知
，
∴
，
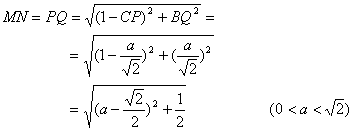
（II）由（I）
所以，当
时，
即当
、
分别为
、
的中点时，
的长最小，最小值为
（III）取的中点
，连结
、
，
∵
，为的中点
∴
，即
即为二面角的平面角
又
，所以，由余弦定理有
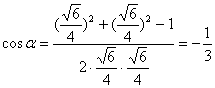
故所求二面角为
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目