题目内容
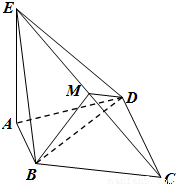
如图,四棱锥 E-ABCD中,EA⊥平面ABCD,AB⊥AD,AB∥DC,AD=AE=CD=2AB,M是EC的中点.(I)求证:平面BCE⊥平面DCE;
(II)求锐二面角M-BD-C平面角的余弦值.
【答案】分析:(I)建立空间直角坐标系,确定平面BCE的法向量、平面DCE的法向量,利用法向量的垂直关系,证明面面垂直;
(II)求得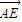 为平面BCD的法向量,平面BDM的法向量
为平面BCD的法向量,平面BDM的法向量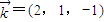 ,利用向量的夹角公式,即可求得结论.
,利用向量的夹角公式,即可求得结论.
解答: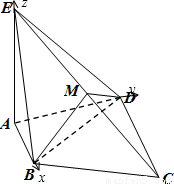 (I)证明:由于平面ABCD,AB⊥AD,可建立以点A为坐标原点,直线AB、AD、AE分别为x,y,z轴的空间直角坐标系.
(I)证明:由于平面ABCD,AB⊥AD,可建立以点A为坐标原点,直线AB、AD、AE分别为x,y,z轴的空间直角坐标系.
设AB=1,则A(0,0,0),B(1,0,0),D(0,2,0),E(0,0,2),C(2,2,0),
∵M是EC的中点,∴M(1,1,1)
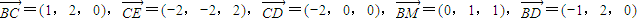
设平面BCE的法向量为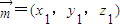 ,平面DCE的法向量为
,平面DCE的法向量为 ,则有:
,则有:
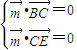 ,∴
,∴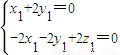
∴可取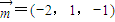
同理: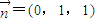
又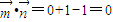 ,∴
,∴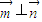 ,
,
∴平面BCE⊥平面DCE
(II)解:由题意可知向量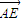 为平面BCD的法向量,设平面BDM的法向量为
为平面BCD的法向量,设平面BDM的法向量为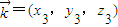
∴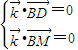 ,∴
,∴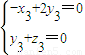
令y3=1,则x3=2,z3=-1
∴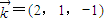
又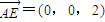 ,∴
,∴ ,
,
∴锐二面角M-BD-C平面角的余弦值为 .
.
点评:本题考查面面垂直,考查向量知识的运用,考查面面角,解题的关键是确定平面的法向量.
(II)求得
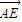 为平面BCD的法向量,平面BDM的法向量
为平面BCD的法向量,平面BDM的法向量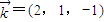 ,利用向量的夹角公式,即可求得结论.
,利用向量的夹角公式,即可求得结论.解答:
 (I)证明:由于平面ABCD,AB⊥AD,可建立以点A为坐标原点,直线AB、AD、AE分别为x,y,z轴的空间直角坐标系.
(I)证明:由于平面ABCD,AB⊥AD,可建立以点A为坐标原点,直线AB、AD、AE分别为x,y,z轴的空间直角坐标系.设AB=1,则A(0,0,0),B(1,0,0),D(0,2,0),E(0,0,2),C(2,2,0),
∵M是EC的中点,∴M(1,1,1)
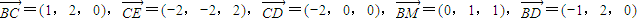
设平面BCE的法向量为
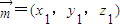 ,平面DCE的法向量为
,平面DCE的法向量为 ,则有:
,则有: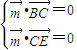 ,∴
,∴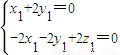
∴可取
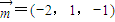
同理:
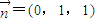
又
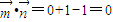 ,∴
,∴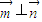 ,
,∴平面BCE⊥平面DCE
(II)解:由题意可知向量
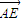 为平面BCD的法向量,设平面BDM的法向量为
为平面BCD的法向量,设平面BDM的法向量为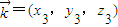
∴
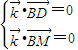 ,∴
,∴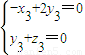
令y3=1,则x3=2,z3=-1
∴
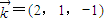
又
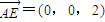 ,∴
,∴ ,
,∴锐二面角M-BD-C平面角的余弦值为
 .
.点评:本题考查面面垂直,考查向量知识的运用,考查面面角,解题的关键是确定平面的法向量.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
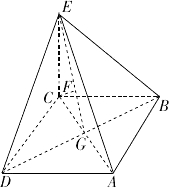 如图,四棱锥E-ABCD中,底面ABCD为正方形,EC⊥平面ABCD,AB=
如图,四棱锥E-ABCD中,底面ABCD为正方形,EC⊥平面ABCD,AB=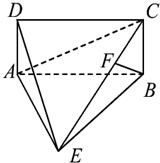 如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,
如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,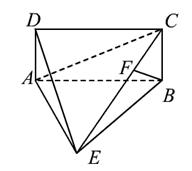
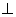 平面ABCD,AE=EB=BC=2,F为CE上的点,且BF
平面ABCD,AE=EB=BC=2,F为CE上的点,且BF
 平面ABCD,AE=EB=BC=2,F为CE上的点,
平面ABCD,AE=EB=BC=2,F为CE上的点,