题目内容
已知数列![]() 是首项为1公差为正的等差数列,数列
是首项为1公差为正的等差数列,数列![]() 是首项为1的等比数列,设
是首项为1的等比数列,设![]()
![]() ,且数列
,且数列![]() 的前三项依次为1,4,12,
的前三项依次为1,4,12,
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
解析:(1)设数列![]() 的公差为d,
的公差为d,![]() 的公比为q,则有题意知
的公比为q,则有题意知
 3分
3分
因为数列![]() 各项为正数,所以d>0
各项为正数,所以d>0
所以把a![]() =1,b
=1,b![]() =1代入方程组解得
=1代入方程组解得![]() 6分
6分
(2)由(1)知等差数列![]() 的前n项和Sn=na
的前n项和Sn=na![]() +
+![]()
![]()
所以![]()
![]()
所以数列![]() 是首项是a
是首项是a![]() =1,公差为
=1,公差为![]() =
=![]() 的等差数列 9分
的等差数列 9分
所以T![]() =n a
=n a![]() +
+![]() =n+
=n+![]() =
=![]() 12分
12分

练习册系列答案
相关题目
 的前n项和为
的前n项和为 ,已知数列
,已知数列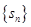 是首项和公比都为3的等比数列,则数列
是首项和公比都为3的等比数列,则数列 =_____________________
=_____________________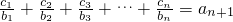 成立求c1+c2+…+c2007的值.
成立求c1+c2+…+c2007的值. 成立求c1+c2+…+c2007的值.
成立求c1+c2+…+c2007的值.