��Ŀ����
����Ŀ��ijУ��һѧ������500�ˣ�Ϊ���˽�ѧ������ʷѧϰ����������ȡ��50��ѧ����������һ����4�ο��Ե���ʷƽ���ɼ�����ͳ�ƣ��õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��������Ƶ���ɵȱ����У�
��1������塢�����Ƶ������ȫƵ�ʷֲ�ֱ��ͼ��
��2����ÿ�������ø��������е�ֵ����������[70��80�����е�ֵ��
75��Ϊ�������Թ��Ƹ�У��һѧ����ʷ�ɼ���ƽ���֣�
��3�����Ƹ�У��һѧ����ʷ�ɼ���70��100�ַ�Χ�ڵ�������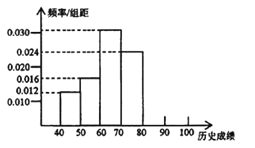
���𰸡��⣺��1������塢�����Ƶ���ֱ�Ϊx��y
������ã�
�������Ƶ����0.024��10��50=12
��x2=12y
��x+y=50����0.012+0.016+0.03+0.024����10��50��x+y=9
��x=6��
y=3��
��ȫƵ�ʷֲ�ֱ��ͼ
��2����У��һѧ����ʷ�ɼ���ƽ����![]() =(45x0.012+55x0.016+65x0.03+75x0.024+95x0.006)=67.6
=(45x0.012+55x0.016+65x0.03+75x0.024+95x0.006)=67.6
��3����У��һѧ����ʷ�ɼ���70��100�ַ�Χ�ڵ�������
500����0.024+0.012+0.006����10=210
����������1������Ƶ�ʷֲ�ֱ��ͼ����������������������������Ƶ�ʣ�����Ƶ�ʳ��������������Ƶ�������õȱ����е������г�����������塢�����Ƶ����
��2�����ø���С���ε��е���Ը������ε���������һѧ����ʷ�ɼ���70��100�ַ�Χ�ڵ�������
�����㾫����������Ĺؼ�����������������������������������������������֪ʶ��������������������ʱ����������ķ����ȽϺ�������ô�������Է�ӳ�������Ϣ�����������õ�����Ϣ����ƫ�����������У�����ƫ���Dz��ɱ���ģ�


