题目内容
已知M是直线3x+4y+8=0上的动点,MA、MB是圆P:(x-1)2+(y-1)2=4的两条切线,A、B为切点,P为圆心,求
•
的最大值
| PE |
| PF |
-
| 4 |
| 9 |
-
.| 4 |
| 9 |
分析:由题意可得
•
=4cos∠EPF,当∠EMF最大时,
•
的值最大.由于当PM和直线3x+4y+8=0垂直时,∠EMF最大,此时,求得PM的值,即可求得cos∠PMF,利用二倍角
公式求得cos∠EPF 的值,从而求得
•
的值最大.
| PE |
| PF |
| PE |
| PF |
公式求得cos∠EPF 的值,从而求得
| PE |
| PF |
解答: 解:由题意可得
解:由题意可得
•
=2×2×cos∠EPF=4cos∠EPF,圆心P(1,1),故要使
•
的值最大,只有∠EPF 最小.
再由四边形MEPF中∠MEP=∠MFP=
可得四边形MEPF是圆内接四边形,故∠EPF+∠EMF=π,故当∠EMF最大时,
•
的值最大.
由于当PM和直线3x+4y+8=0垂直时,∠EMF最大,此时,切线ME=MF,∠EPF=2∠MPF,PM等于圆心P到直线的距离
=3.
cos∠PMF=
=
,cos∠EPF=cos(2∠MPF)=2cos2∠MPF-1=
-1=-
,
故
•
的值最大为 4cos∠EPF=4×(-
)=-
,
故答案为-
.
 解:由题意可得
解:由题意可得 | PE |
| PF |
| PE |
| PF |
再由四边形MEPF中∠MEP=∠MFP=
| π |
| 2 |
| PE |
| PF |
由于当PM和直线3x+4y+8=0垂直时,∠EMF最大,此时,切线ME=MF,∠EPF=2∠MPF,PM等于圆心P到直线的距离
| |3+4+8| | ||
|
cos∠PMF=
| PF |
| PM |
| 2 |
| 3 |
| 8 |
| 9 |
| 1 |
| 9 |
故
| PE |
| PF |
| 1 |
| 9 |
| 4 |
| 9 |
故答案为-
| 4 |
| 9 |
点评:本题主要考查两个向量的数量积的定义,圆的切线性质,二倍角公式的应用,体现了数形结合的数学思想,属于中档题.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
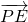 •
• 的最大值________.
的最大值________. •
• 的最大值 .
的最大值 . •
• 的最大值 .
的最大值 .