题目内容
关于 的方程
的方程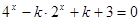 只有一个实数解,则实数
只有一个实数解,则实数 的取值范围是_______.
的取值范围是_______.
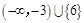 .
.
解析试题分析:令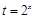 ,方程
,方程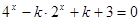 可化为
可化为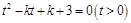 .要使方程
.要使方程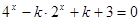 只有一个实数解,则方程
只有一个实数解,则方程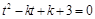 两根一正一负或有两相等的正根,
两根一正一负或有两相等的正根,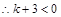 或
或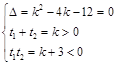 ,解得
,解得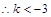 或
或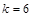 .
.
考点:函数与方程.

练习册系列答案
相关题目
题目内容
关于 的方程
的方程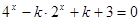 只有一个实数解,则实数
只有一个实数解,则实数 的取值范围是_______.
的取值范围是_______.
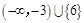 .
.
解析试题分析:令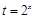 ,方程
,方程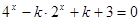 可化为
可化为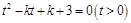 .要使方程
.要使方程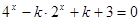 只有一个实数解,则方程
只有一个实数解,则方程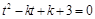 两根一正一负或有两相等的正根,
两根一正一负或有两相等的正根,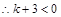 或
或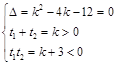 ,解得
,解得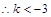 或
或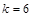 .
.
考点:函数与方程.
